题目内容
正四棱锥的每条棱长均为2,则该四棱锥的侧面积为 .
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:根据正四棱锥几何性质,4个侧面为全等的三角形,再根据正三角形的面积公式求解.
解答:
解:∵正四棱锥的每条棱长均为2,
∴4个侧面为全等的三角形,
∴4×
×22=4
,
故答案为:4
,
∴4个侧面为全等的三角形,
∴4×
| ||
| 4 |
| 3 |
故答案为:4
| 3 |
点评:本题考查了正四棱锥几何性质,体积面积公式,属于容易题.

练习册系列答案
相关题目
已知△ABC满足c=2acosB,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
已知空间四边形ABCD,E,F,G,H分别边AB,BC,CD,DA的中点,则EG与FH位置关系是( )
| A、相交 | B、平行 | C、异面 | D、重合 |
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
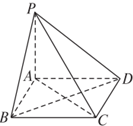

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
双曲线
-
=1的离心率e∈(1,2),则实数k的取值范围是( )
| x2 |
| 4 |
| y2 |
| k |
| A、(0,4) | ||
| B、(1,1) | ||
C、(0,2
| ||
| D、(0,12) |
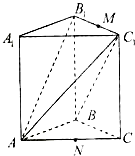 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.