题目内容
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
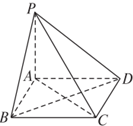

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:由于PA垂直于正方形ABCD所在平面,所以PA所在的平面与底面垂直,又ABCD为正方形,故又存在一些线线垂直关系,从而可以得到线面垂直,进而可以判定面面垂直.
解答:
证明:由于CD⊥AD,由PA垂直于正方形ABCD所在平面,所以CD⊥PA,易证CD⊥平面PAD,则平面PCD⊥平面PAD;
由于BC⊥AB,由PA垂直于正方形ABCD所在平面,所以BC⊥PA,易证BC⊥平面PAB,则平面PAB⊥平面PBC;
又AD∥BC,故AD⊥平面PAB,则平面PAD⊥平面PAB.
故选:B.
由于BC⊥AB,由PA垂直于正方形ABCD所在平面,所以BC⊥PA,易证BC⊥平面PAB,则平面PAB⊥平面PBC;
又AD∥BC,故AD⊥平面PAB,则平面PAD⊥平面PAB.
故选:B.
点评:本题考查面面垂直的判定定理的应用,要注意转化思想的应用,将面面垂直转化为线面垂直.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,a,b,c分别为角A、B、C的对边,a=4,b=4
,∠A=30°,则∠B等于( )
| 3 |
| A、30° |
| B、30°或150° |
| C、60° |
| D、60°或120° |
甲乙两种小麦试验品种x年的平均产量如下表:
则根据这组数据估计哪一品种小麦产量较稳定( )
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| A、甲乙稳定性相同 | B、乙较稳定 |
| C、甲较稳定 | D、无法比较 |
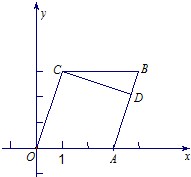 如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.
如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.