题目内容
已知空间四边形ABCD，E，F，G，H分别边AB，BC，CD，DA的中点，则EG与FH位置关系是（ ）
| A、相交 | B、平行 | C、异面 | D、重合 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：连接EF，FG，GH，HE，EG，FH．运用中位线定理，即可得到EH∥FG，EH=FG，即有四边形EFGH为平行四边形，即可判断EG与FH的位置关系．
解答：
解：如图，连接EF，FG，GH，HE，EG，FH．
由于E，H为AB、AD的中点，则EH∥BD，EH=
BD，
由于F，G为BC，CD的中点，则FG∥BD，FG=
BD，
则有EH∥FG，EH=FG，
即有四边形EFGH为平行四边形，则EG和FH相交．
故选A．
解：如图，连接EF，FG，GH，HE，EG，FH．由于E，H为AB、AD的中点，则EH∥BD，EH=
| 1 |
| 2 |
由于F，G为BC，CD的中点，则FG∥BD，FG=
| 1 |
| 2 |
则有EH∥FG，EH=FG，
即有四边形EFGH为平行四边形，则EG和FH相交．
故选A．
点评：本题考查空间直线与直线的位置关系，考查推理能力，属于基础题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
若集合A={1，2}，B={2，4}，则A∪B=（ ）
| A、{2} |
| B、{3} |
| C、{1，2，4} |
| D、{0，1，2} |
已知G点是△ABC的重心，
⊥
，
+
=
，则λ的值为（ ）
| AG |
| BG |
| 1 |
| tanA |
| 1 |
| tanB |
| 2λ |
| tanC |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
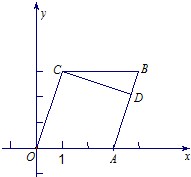如图，在平行四边形OABC中，点A（3，0），C（1，3），过点C做CD⊥AB于点D．