题目内容
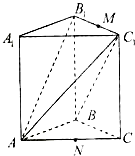 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.(1)求三棱锥B1-ABC1的体积;
(2)求MN与底面ABC所成的角.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用等体积,计算三棱锥B1-ABC1的体积;
(2)取BC的中点P,连接MP、NP,根据三角形中位线定理,得MP∥BB1,则MP⊥平面ABC,解三角形MNP即可得到MN的长,确定MN与底面所成的角为∠MNP,解三角形MNP即可得到MN与底面ABC所成的角.
(2)取BC的中点P,连接MP、NP,根据三角形中位线定理,得MP∥BB1,则MP⊥平面ABC,解三角形MNP即可得到MN的长,确定MN与底面所成的角为∠MNP,解三角形MNP即可得到MN与底面ABC所成的角.
解答:
解:(1)VB1-ABC1=VC1-ABC=
•
•4•4•3=8.
(2)取BC的中点P,连接MP、NP,则MP∥BB1,

∴MP⊥平面ABC,又NP?平面ABC,
∴MP⊥NP,MN与底面所成的角为∠MNP
∵PN=2,MP=3,
∴MN=
=
.
∵NP=2,
∴tan∠MNP=
,
∴∠MNP=arctan
.
| 1 |
| 3 |
| 1 |
| 2 |
(2)取BC的中点P,连接MP、NP,则MP∥BB1,

∴MP⊥平面ABC,又NP?平面ABC,
∴MP⊥NP,MN与底面所成的角为∠MNP
∵PN=2,MP=3,
∴MN=
| 4+9 |
| 13 |
∵NP=2,
∴tan∠MNP=
| 3 |
| 2 |
∴∠MNP=arctan
| 3 |
| 2 |
点评:本题考查的知识点是直线与平面所成的角,根据线面夹角的定义,求出线面夹角是解答本题的关键.

练习册系列答案
相关题目
不等式
<1的解集是( )
| 1 |
| x |
| A、{x|x>1} |
| B、{x|x<0} |
| C、{x|x>1或x<0} |
| D、{x|0<x<1} |
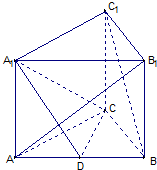 如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.
如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.