题目内容
已知椭圆C:
+y2=1,
(1)若直线l过点Q(1,1),交椭圆C于A、B两点,求直线l的方程使得Q为AB的中点;
(2)定点M(0,2),P为椭圆C上任意一点,求线段PM的最大值.
| x2 |
| 4 |
(1)若直线l过点Q(1,1),交椭圆C于A、B两点,求直线l的方程使得Q为AB的中点;
(2)定点M(0,2),P为椭圆C上任意一点,求线段PM的最大值.
考点:椭圆的简单性质,直线的点斜式方程
专题:圆锥曲线的定义、性质与方程
分析:(1)利用点差法求直线的方程;
(2)设出椭圆上任意一点的参数坐标,由两点间的距离公式写出|PA|,利用配方法求其最大值.
(2)设出椭圆上任意一点的参数坐标,由两点间的距离公式写出|PA|,利用配方法求其最大值.
解答:
解:(1)设A((x1,y1),B(x2,y2),
则:
+y12=1,
+y22=1,
两式相减得:
+(y1-y2)(y1+y2)=0
因为Q(1,1)为AB的中点,
所以x1+x2=2,y1+y2=2,
所以
=-
,
故l的方程为:x+4y-5=0…7分
(2)因为椭圆C:
+y2=1,
设P点坐标是(2cost,sint)
则|PA|=
=
,
∴当sint=
时,|PA|max=
=
,
故答案为:
…14分.
则:
| x12 |
| 4 |
| x22 |
| 4 |
两式相减得:
| (x1-x2)(x1+x2) |
| 4 |
因为Q(1,1)为AB的中点,
所以x1+x2=2,y1+y2=2,
所以
| y1-y2 |
| x1-x2 |
| 1 |
| 4 |
故l的方程为:x+4y-5=0…7分
(2)因为椭圆C:
| x2 |
| 4 |
设P点坐标是(2cost,sint)
则|PA|=
| (2cost)2+(sint-2)2 |
=
-3(sint-
|
∴当sint=
| 2 |
| 3 |
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查了椭圆的简单几何性质,考查了椭圆的参数方程,训练了函数最值的求法,是中档题.

练习册系列答案
相关题目
若点P在
的终边上,且|OP|=2,则点P的坐标( )
| 5π |
| 3 |
A、(1,-
| ||
B、(
| ||
C、(-1,-
| ||
D、(-1,
|
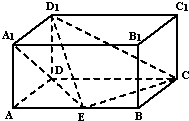 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点 地面上有两个同心圆(如图),其半径分别为1,2.若向图中最大的圆内投点且投到图中阴影区域的概率为
地面上有两个同心圆(如图),其半径分别为1,2.若向图中最大的圆内投点且投到图中阴影区域的概率为