题目内容
已知正三棱锥的高比底面边长小4,且其外接球的表面积为196π,则该正三棱锥的体积为 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得该三棱锥外接球的半径为7,H是正△ABC的中心,AH=
a×
=
a,则球心到底面中心的距离为|a-4-7|,由勾股定理得a=12,由此能求出该正三棱锥的体积.
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
解答:
解:如图,设球半径为r,正三棱锥的底面边长为a,则高SH=a-4,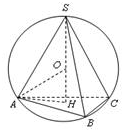
∵正三棱锥的外接球的表面积为196π,
∴4πr2=196π,解得r=7,即该三棱锥外接球的半径为7,
∵H是正△ABC的中心,∴AH=
a×
=
a,
则球心到底面中心的距离为|a-4-7|,
在Rt△OHA中,由勾股定理得,72=(a-4-7)2+(
a)2,
解得a=12,或a=
,(舍)
∴a=12,SH=8,
∴该正三棱锥的体积为:
V=
×
×a2×sin60°×SH=
×
×a2×SH=96
.
故答案为:96
.

∵正三棱锥的外接球的表面积为196π,
∴4πr2=196π,解得r=7,即该三棱锥外接球的半径为7,
∵H是正△ABC的中心,∴AH=
| ||
| 2 |
| 2 |
| 3 |
| ||
| 3 |
则球心到底面中心的距离为|a-4-7|,
在Rt△OHA中,由勾股定理得,72=(a-4-7)2+(
| ||
| 3 |
解得a=12,或a=
| 9 |
| 2 |
∴a=12,SH=8,
∴该正三棱锥的体积为:
V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
故答案为:96
| 3 |
点评:本题考查三棱锥的体积的求法,则中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知圆x2+(y-1)2=2上任一点P(x,y),其坐标均使得不等式x+y+m≥0恒成立,则 实数m的取值范围是( )
| A、[1,+∞) |
| B、(-∞,1] |
| C、[-3,+∞) |
| D、(-∞,-3] |
圆柱的轴截面(经过圆柱的轴所作的截面)是边长为5cm的正方形ABCD,则圆柱侧面上从A到C的最短距离为( )
| A、10 cm | ||||
B、
| ||||
C、5
| ||||
D、5
|
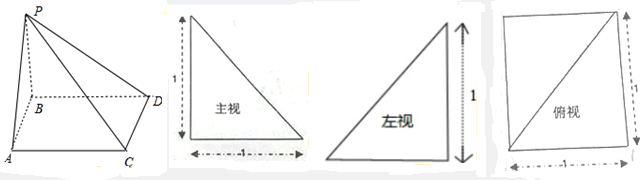 (1)求四棱锥的体积和表面积;
(1)求四棱锥的体积和表面积;