题目内容
已知正实数a,b,c满足a+b+c=1,
+
+
=10,则abc的取值范围是 .
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点:平均值不等式在函数极值中的应用
专题:计算题,不等式的解法及应用
分析:由a+b+c=1结合基本不等式,可得0<ab+bc+ac≤
,由
+
+
=10,可得abc=
(ab+bc+ac),即可得出结论.
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| 10 |
解答:
解:由a+b+c=1可得:1=(a+b+c)2=a2+b2+c2 +2ab+2bc+2ac≥3(ab+bc+ac),
故有0<ab+bc+ac≤
.
∵
+
+
=10,
∴abc=
(ab+bc+ac),
∴0<abc≤
,
故答案为:(0,
].
故有0<ab+bc+ac≤
| 1 |
| 3 |
∵
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∴abc=
| 1 |
| 10 |
∴0<abc≤
| 1 |
| 30 |
故答案为:(0,
| 1 |
| 30 |
点评:本题考查基本不等式的运用,考查学生分析解决问题的能力,确定0<ab+bc+ac≤
是关键.
| 1 |
| 3 |

练习册系列答案
相关题目
若直线y=2ax-2与y=(a+2)x+1平行,则a=( )
| A、2 | B、1 | C、-1 | D、0 |
已知椭圆
+
=1(a>b>0)的左顶点为A,左焦点为F,上顶点为B,且∠BAO+∠BFO=90°(O为坐标原点),则椭圆的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是
如图,正方体ABCD-A1B1C1D1中,AB=2,则三棱锥A-A1B1C的体积是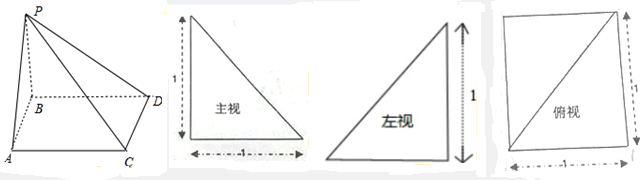 (1)求四棱锥的体积和表面积;
(1)求四棱锥的体积和表面积;