题目内容
3.已知数列{an}中,a1=1,an=3an-1+4(n∈N*且n≥2),则数列{an}通项公式an=3n-2.分析 a1=1,an=3an-1+4(n∈N*且n≥2),变形为an+2=3(an-1+2),利用等比数列的通项公式即可得出.
解答 解:∵a1=1,an=3an-1+4(n∈N*且n≥2),
变形为an+2=3(an-1+2),
∴数列{an}是等比数列,首项为3,公比为3.
∴an+2=3n,
解得an=3n-2.
故答案为:3n-2.
点评 本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点.若椭圆C上存在点P,使得线段PF1的中垂线恰好过焦点F2,则椭圆C离心率的取值范围是( )
| A. | [$\frac{2}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{3}$,1) | D. | (0,$\frac{1}{3}$] |
14.已知A={x|x2-2x-3≤0},$B=\left\{{y\left|{y=}\right.}\right.\left.{\sqrt{{x^2}+3}}\right\}$,则A∩B=( )
| A. | $[{1,\sqrt{2}}]$ | B. | $[{\sqrt{2},\sqrt{3}}]$ | C. | $[{\sqrt{3},3}]$ | D. | $[{2,\sqrt{3}}]$ |
18.已知函数f(x)=x3+sinx+1,则f(-2015)+f(-2014)+f(-2013)+…+f(2014)+f(2015)=( )
| A. | 0 | B. | 2014 | C. | 4028 | D. | 4031 |
8.已知a>0,且a≠1,则函数f(x)=ax-1+1的图象恒过定点( )
| A. | (1,1) | B. | (1,2) | C. | (2,1) | D. | (1,0) |
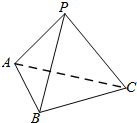 如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.