题目内容
13.已知F1、F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点.若椭圆C上存在点P,使得线段PF1的中垂线恰好过焦点F2,则椭圆C离心率的取值范围是( )| A. | [$\frac{2}{3}$,1) | B. | [$\frac{1}{3}$,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{3}$,1) | D. | (0,$\frac{1}{3}$] |
分析 设P(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1.则线段PF1的中点M$(\frac{{x}_{0}-c}{2},\frac{{y}_{0}}{2})$.由于线段PF1的中垂线恰好过焦点F2,可得${k}_{P{F}_{1}}{k}_{{F}_{2}M}$=-1,化简解得x0=$\frac{{a}^{2}-2ac}{c}$,利用-a≤x0≤a,解出即可得出.
解答 解:设P(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1.
则线段PF1的中点M$(\frac{{x}_{0}-c}{2},\frac{{y}_{0}}{2})$.
∵线段PF1的中垂线恰好过焦点F2,
∴${k}_{P{F}_{1}}{k}_{{F}_{2}M}$=$\frac{{y}_{0}}{{x}_{0}+c}$•$\frac{\frac{{y}_{0}}{2}-0}{\frac{{x}_{0}-c}{2}-c}$=-1,
化为:$\frac{{y}_{0}^{2}}{({x}_{0}+c)({x}_{0}-3c)}=-1$,
∴${b}^{2}(1-\frac{{x}_{0}^{2}}{{a}^{2}})$+(x0+c)(x0-3c)=0,
化为:${c}^{2}{x}_{0}^{2}$-2a2cx0+b2a2-3a2c2=0,
解得x0=$\frac{{a}^{2}-2ac}{c}$,
由于-a≤x0≤a,
∴-a≤$\frac{{a}^{2}-2ac}{c}$≤a,又0<e<1,
解得$\frac{1}{3}≤e$<1.
故选:C.
点评 本题考查了椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.

| A. | $[\frac{3}{2},3]$ | B. | $[\frac{3}{2},\frac{5}{2}]$ | C. | $[\frac{5}{2},3]$ | D. | $[\frac{3}{2},5]$ |
| A. | (-∞,-2) | B. | (-5,-2) | C. | [-5,-2] | D. | (-∞,-2] |

| A. | 2 450 | B. | 2 500 | C. | 2 550 | D. | 2 652 |
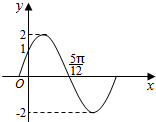 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).