题目内容
11.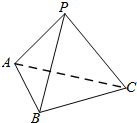 如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
分析 以PA、PB、PC为过同一顶点的三条棱,作长方体如图,则长方体的外接球同时也是三棱锥P-ABC外接球.算出长方体的对角线即为球直径,结合球的体积公式,可算出棱锥外接球的体积.
解答  解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图
解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球.
∵长方体的对角线长为$\sqrt{1+4+4}$=3,
∴球直径为3,半径R=$\frac{3}{2}$,
因此,棱锥外接球的体积为$\frac{4}{3}$πR3=$\frac{9}{2}π$.
故答案为:$\frac{9}{2}π$.
点评 本题给出三棱锥的三条侧棱两两垂直,求棱锥外接球的体积,着重考查了长方体对角线公式和球的表面积计算等知识,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.如果执行如图所示的程序框图,那么输出的S等于( )


| A. | 2 450 | B. | 2 500 | C. | 2 550 | D. | 2 652 |
6.已知向量$\overrightarrow a=({2,1})$,$\overrightarrow{b}$=(-2,k2),则k=2是$\overrightarrow{a}$⊥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.若a>b,则下列选项一定成立的是( )
| A. | a2>b2 | B. | ac>bc | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ac2≥bc2 |