题目内容
15.已知函数$f(x)=a+\frac{1}{{{2^x}+1}}$.(1)当函数f(x)为奇函数时,求a的值;
(2)判断函数f(x)在区间(-∞,+∞)上是增函数还是减函数,并用定义证明你的结论.
分析 (1)求出函数的定义域,利用函数f(x)为奇函数,f(0)=0,即可求a的值;
(2判断函数f(x)在区间(-∞,+∞)上是减函数,然后用定义证明即可.
解答 解:(1)函数f(x)的定义域为R,
由于定义域为R的奇函数有f(0)=0,…(4分)
故$f(0)=a+\frac{1}{{{2^0}+1}}=0$,解得$a=-\frac{1}{2}$.…(7分)
(2)函数f(x)在区间(-∞,+∞)上是减函数. …(8分)
证明:任取x1<x2,有${2^{x_2}}-{2^{x_1}}>0$,
则$f({x_1})-f({x_2})=(a+\frac{1}{{{2^{x_1}}+1}})-(a+\frac{1}{{{2^{x_2}}+1}})$=$\frac{1}{{{2^{x_1}}+1}}-\frac{1}{{{2^{x_2}}+1}}=\frac{{{2^{x_2}}-{2^{x_1}}}}{{({2^{x_1}}+1)({2^{x_2}}+1)}}>0$,…(13分)
即f(x1)<f(x2),所以函数f(x)在区间(-∞,+∞)上是减函数. …(15分)
(注:在本小题中若取$a=-\frac{1}{2}$证明,其它无误,则扣2分)
点评 本题考查函数的奇偶性的应用以及函数的单调性的证明,考查计算能力.

练习册系列答案
相关题目
6.已知向量$\overrightarrow a=({2,1})$,$\overrightarrow{b}$=(-2,k2),则k=2是$\overrightarrow{a}$⊥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
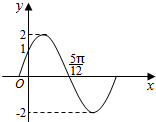 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).