题目内容
已知数列{an}满足:对于n∈N,都有an+1=
.
(1)若a1=5,求an;
(2)若a1=3,求an.
(3)若a1=6,求an.
(4)当a1取哪些值时,无穷数列{an}不存在?
| 13an-25 |
| an+3 |
(1)若a1=5,求an;
(2)若a1=3,求an.
(3)若a1=6,求an.
(4)当a1取哪些值时,无穷数列{an}不存在?
考点:数列递推式
专题:等差数列与等比数列
分析:作特征方程x=
,变形,得x2-10x+25=0,特征方程有两个相同的特征根λ=5.由此结合已知条件能求出结果.
| 13x-25 |
| x+3 |
解答:
解:作特征方程x=
,变形,得x2-10x+25=0,
特征方程有两个相同的特征根λ=5,
(1)∵a1=5,∴a1=λ,
∴对于n∈N*,都有an=λ=5.
(2)∵a1=3,∴a1≠λ,
∴bn=
+(n-1)•
=
+
=-
+
,
令bn=0,得n=5,故数列{an}从第5项起都不存在,
当n≤4时,n∈N*时,an=
+λ=
(3)∵a1=6,∴a1≠λ,
∴bn=
+
=1+
,
令bn=0,得n=7,
∴an=
+λ=
+5=
,n∈N*.
(4)a1=-3时,数列从第三项就不存在,a1=5时,{an}存在,
当a1≠λ=5时,bn=
+
,n∈N*,
令bn=0,则a1=
,n∈N*,且n≥2,
∴当a1=
,n∈N*,且n≥2时,数列{an}从第n项开始便不存在.
∴当a1在集合{-3,或
,n∈N*,且n≥2}上取值时,无穷数列{an}都不存在.
| 13x-25 |
| x+3 |
特征方程有两个相同的特征根λ=5,
(1)∵a1=5,∴a1=λ,
∴对于n∈N*,都有an=λ=5.
(2)∵a1=3,∴a1≠λ,
∴bn=
| 1 |
| a1-λ |
| 1 |
| 13-1•5 |
=
| 1 |
| 3-5 |
| n-1 |
| 8 |
=-
| 1 |
| 2 |
| n-1 |
| 8 |
令bn=0,得n=5,故数列{an}从第5项起都不存在,
当n≤4时,n∈N*时,an=
| 1 |
| bn |
| 5n-17 |
| n-5 |
(3)∵a1=6,∴a1≠λ,
∴bn=
| 1 |
| a1-λ |
| n-1 |
| 8 |
| n-1 |
| 8 |
令bn=0,得n=7,
∴an=
| 1 |
| bn |
| 1 | ||
1+
|
| 5n+43 |
| n+7 |
(4)a1=-3时,数列从第三项就不存在,a1=5时,{an}存在,
当a1≠λ=5时,bn=
| 1 |
| a1-5 |
| n-1 |
| 8 |
令bn=0,则a1=
| 5n-13 |
| n-1 |
∴当a1=
| 5n-13 |
| n-1 |
∴当a1在集合{-3,或
| 5n-13 |
| n-1 |
点评:本题考查数列的通项公式的求法,解题时要认真审题,注意特征方程和特征根的合理运用.

练习册系列答案
相关题目
已知函数f(x)=xα,α∈{-1,
,1,2,3},若f(x)是区间(-∞,+∞)上的增函数,则α的所有可能取值为( )
| 1 |
| 2 |
| A、{1,3} | ||
B、{
| ||
| C、{1,2,3} | ||
D、{-1,
|
函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,函数f(x)的值域为( )
| A、{-2,-1,0,1,2} |
| B、{-3,-2,-1,0,1,2} |
| C、{-2,-1,0,1,2,3} |
| D、{-3,-2,-1,0,1,2,3} |
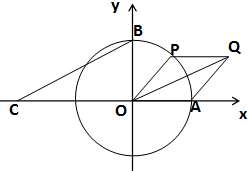 如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.