题目内容
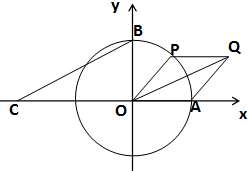 如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A、B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),点C坐标为(-2,0),平行四边形OAQP的面积为S.(1)求t=
| OA |
| OQ |
(2)若CB∥OP,求sin(2θ-
| π |
| 3 |
考点:两角和与差的正弦函数,平面向量的基本定理及其意义
专题:三角函数的求值
分析:(1)利用向量的坐标公式求出t=
•
+S的表达式,利用辅助角将函数进行化简,即可求出函数的最大值;
(2)利用直线平行转化为向量平行,利用两角和差的正弦公式进行求解即可.
| OA |
| OQ |
(2)利用直线平行转化为向量平行,利用两角和差的正弦公式进行求解即可.
解答:
解:(1)∵
=(1,0),P(cosθ,sinθ),∴
=(1+cosθ,sinθ),
∴
•
=1+cosθ,
而S=2×
|
|•|
|sinθ=sinθ,
∴t=
•
+S=1+cosθ+sinθ=1+
sin(θ+
),
∵0<θ<π,∴当θ=
时,t=
•
+S取得最大值为1+
;
(2)
=(2,1),
=(cosθ,sinθ),
由CB∥OP得cosθ=2sinθ,
又0<θ<π,
结合sin2θ+cos2θ=1得sinθ=
,cosθ=
,sin2θ=
,cos2θ=
,
∴sin(2θ-
)=sin2θ•cos
-cos2θ•sin
=
.
| OA |
| OQ |
∴
| OA |
| OQ |
而S=2×
| 1 |
| 2 |
| OA |
| OP |
∴t=
| OA |
| OQ |
| 2 |
| π |
| 4 |
∵0<θ<π,∴当θ=
| π |
| 4 |
| OA |
| OQ |
| 2 |
(2)
| CB |
| OP |
由CB∥OP得cosθ=2sinθ,
又0<θ<π,
结合sin2θ+cos2θ=1得sinθ=
| ||
| 5 |
2
| ||
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴sin(2θ-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
4-3
| ||
| 10 |
点评:本题主要考查三角函数的化简和求值,利用向量的坐标公式求出向量坐标是解决本题的关键.

练习册系列答案
相关题目
等差数列{an}中,a1=1,a2=3,数列{
}的前n项和为
,则n的值为( )
| 1 |
| anan+1 |
| 15 |
| 31 |
| A、15 | B、16 | C、17 | D、18 |
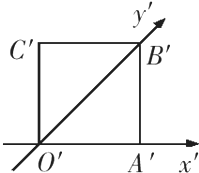 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )
一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,如图则原平面图形的面积为( )