题目内容
判断下列函数的奇偶性:
①f(x)=(x-1)2
②f(x)=
.
①f(x)=(x-1)2
②f(x)=
| ||
| |x+2|-2 |
考点:函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:先求函数的定义域,判断函数的定义域是否关于原点对称,再利用函数奇偶性的定义即可得到结论.
解答:
解:①函数f(x)的定义域为R,关于原点对称,
f(-x)=(-x-1)2=(x+1)2≠f(x),且f(-x)≠-f(x),
则函数f(x)不是奇函数,也不是偶函数;
②由1-x2≥0且|x+2|-2≠0,解得,-1≤x≤1且x≠0.
函数f(x)的定义域为{x|-1≤x≤1且x≠0},关于原点对称.
f(x)即化简为f(x)=
,
由于f(-x)=
=-
=-f(x),
则函数f(x)为奇函数.
f(-x)=(-x-1)2=(x+1)2≠f(x),且f(-x)≠-f(x),
则函数f(x)不是奇函数,也不是偶函数;
②由1-x2≥0且|x+2|-2≠0,解得,-1≤x≤1且x≠0.
函数f(x)的定义域为{x|-1≤x≤1且x≠0},关于原点对称.
f(x)即化简为f(x)=
| ||
| x |
由于f(-x)=
| ||
| -x |
| ||
| x |
则函数f(x)为奇函数.
点评:本题主要考查函数的奇偶性的判断,先求出函数的定义域是解决本题的关键.

练习册系列答案
相关题目
设全集为R,集合M={x|log2(x-1)<1},则∁RM=( )
| A、[3,+∞) |
| B、(-∞,1]∪[2,+∞) |
| C、(-∞,1]∪[3,+∞) |
| D、(-∞,0]∪[2,+∞) |
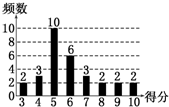 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为. |
| x |
A、me=m0=
| ||
B、me=m0<
| ||
C、me<m0<
| ||
D、m0<me<
|