题目内容
15.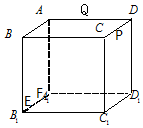 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )| A. | 与x,y,z都有关 | B. | 与x有关,与y,z无关 | ||
| C. | 与y有关,与x,z无关 | D. | 与z有关,与x,y无关 |
分析 △EFQ的面A1B1CD面积的$\frac{1}{4}$,当P点变化时,会导致四面体体积的变化.由此求出四面体PEFQ的体积与z有关,与x,y无关.
解答 解:从图中可以分析出:
△EFQ的面积永远不变,为面A1B1CD面积的$\frac{1}{4}$,
而当P点变化时,
它到面A1B1CD的距离是变化的,
因此会导致四面体体积的变化.
故若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),
则四面体PEFQ的体积与z有关,与x,y无关.
故选:D.
点评 本题考查命题真假的判断,是中档题,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想.

练习册系列答案
相关题目
5.已知f(x)是定义在R上的奇函数,且f(x)=f(x+2),当x∈(0,1)时,f(x)=tan(x-$\frac{π}{6}$),则函数f(x)在区间[0,4]上的零点个数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
6.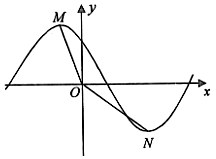 将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )
将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )
 将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )
将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )| A. | 1-$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | -2+$\sqrt{3}$ |
5.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点A作倾斜角为45°的直线l,l交y轴于点B,交双曲线的一条渐近线于点C,若$\overrightarrow{AB}$=$\overrightarrow{BC}$,则该双曲线的离心率为( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |