题目内容
5.已知f(x)是定义在R上的奇函数,且f(x)=f(x+2),当x∈(0,1)时,f(x)=tan(x-$\frac{π}{6}$),则函数f(x)在区间[0,4]上的零点个数是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由题意可推出f(x)在[0,4]上的零点为0,2,4,$\frac{π}{6}$,2-$\frac{π}{6}$,4-$\frac{π}{6}$,即可得出结论.
解答 解:∵当x∈(0,1)时,f(x)=tan(x-$\frac{π}{6}$),
∴f(x)在(0,1)上零点为$\frac{π}{6}$,
又∵函数f(x)是奇函数,
∴f(x)在(-1,0)上零点为-$\frac{π}{6}$,
又∵f(x+2)=f(x),
∴f(x)在[0,4]上的零点为0,2,4,$\frac{π}{6}$,2-$\frac{π}{6}$,4-$\frac{π}{6}$,
故f(x)在[0,4]上的零点个数是6;
故选:A.
点评 本题考查了函数的零点的个数的判断,同时考查了函数的性质的综合应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设$f(x)=\left\{\begin{array}{l}{x^2}({0≤x<1})\\ 2-x({1≤x≤2})\end{array}\right.$则$\int_0^2{f(x)}dx$等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 不存在 |
20.高三年级有8个班级,分派4位数学老师任教,每个教师教两个班,则不同的分派方法有( )
| A. | ${P}_{8}^{2}$${P}_{6}^{2}$${P}_{4}^{2}$${P}_{2}^{2}$ | B. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$ | ||
| C. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$${P}_{4}^{4}$ | D. | $\frac{C_8^2C_6^2C_4^2C_2^2}{4!}$ |
10.已知矩形ABCD中,AB=6,BC=4,E,F分别是AB,CD上两动点,且AE=DF,把四边形BCFE沿EF折起,使平面BCFE⊥平面ABCD,若折得的几何体的体积最大,则该几何体外接球的体积为( )
| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
15.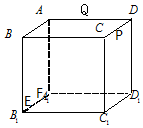 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )| A. | 与x,y,z都有关 | B. | 与x有关,与y,z无关 | ||
| C. | 与y有关,与x,z无关 | D. | 与z有关,与x,y无关 |
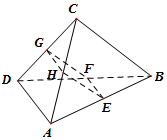 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC