题目内容
2.已知0<c<1,a>b>1,下列不等式成立的是( )| A. | ca>cb | B. | $\frac{a}{a-c}>\frac{b}{b-c}$ | C. | bac>abc | D. | logac>logbc |
分析 根据指数函数,对数函数,幂函数的单调性,结合不等式的基本性质,逐一分析四个答案的真假,可得结论.
解答 解:∵0<c<1,a>b>1,
故ca<cb,故A不成立;
故ac>bc,ab-bc>ab-ac,即b(a-c)>a(b-c),即$\frac{a}{a-c}<\frac{b}{b-c}$,故B不成立;
ac-1>bc-1,ab>0,故bac<abc,故C不成立;
logca<logcb<0,故logac>logbc,故D成立,
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了不等式的基本性质,指数函数,对数函数,幂函数的单调性,难度中档.

练习册系列答案
相关题目
14.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1的直线l与E的左支交于P,Q两点,若|PF1|=2|F1Q|,且F2Q⊥PQ,则E的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{17}}{3}$ |
3.若函数f(x)=lnx-ax+1,a∈R有两个零点,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (0,1) | C. | (-1,1) | D. | (1,2) |
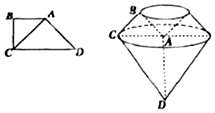 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.