题目内容
15.已知等差数列{an}满足a3+a13-a8=2,则{an}的前15项和S15=( )| A. | 60 | B. | 30 | C. | 15 | D. | 10 |
分析 由等差数列通项公式求出a1+7d=a8=2由此能求出{an}的前15项和S15.
解答 解:∵等差数列{an}满足a3+a13-a8=2,
∴a1+2d+a1+12d-(a1+7d)=2,
即a1+7d=a8=2
∴{an}的前15项和S15=$\frac{15}{2}({a}_{1}+{a}_{15})$=$\frac{15}{2}×2{a}_{8}$=15a8=30
故选:B
点评 本题考查等差数列的前15项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
14.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1的直线l与E的左支交于P,Q两点,若|PF1|=2|F1Q|,且F2Q⊥PQ,则E的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{17}}{3}$ |
3.若函数f(x)=lnx-ax+1,a∈R有两个零点,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (0,1) | C. | (-1,1) | D. | (1,2) |
20.《张邱建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈,问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织九匹三丈,问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布约有( )
| A. | 0.55尺 | B. | 0.53尺 | C. | 0.52尺 | D. | 0.5尺 |
5.平面α截半径为2的球O所得的截面圆的面积为π,则球心到O平面α的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
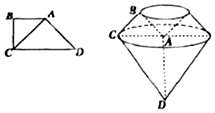 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体. 如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为4的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.