题目内容
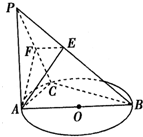 如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC,
正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:分别根据线面垂直和面面垂直的判定定理和性质定理分别进行证明四个结论的真假,最后综合讨论结果,可得答案.
解答:
解:∵AB是⊙O的直径,
∴AC⊥BC,
∵PA⊥⊙O所在平面,
∴PA⊥⊙O所在平面内的所有直线,
∴PA⊥AC,PA⊥AB,PA⊥BC,
∴BC⊥面PAC,
∴BC⊥PC,
∵F是点A在PC上的射影,
∴AF⊥PC,
∵AF∩PC=F,
∴PC⊥面PAC,
∴AF⊥BC,
又AF⊥PC,
∴AF⊥面PBC,
∴AF⊥PB,∴①正确;
∵AF⊥面PBC,
BC?面PBC,
∴AF⊥BC∴③正确.
∵AF⊥PB,AE⊥PB,AF∩AE=A,
∴PB⊥面AEF,
∴EF⊥PB,
∴②正确.
∵AF⊥面PBC,
∴若AE⊥BC,
则AE⊥面PBC,
此时E,F重合,与已知矛盾.∴④错误;
故命题①②③正确,
故选:C
∴AC⊥BC,
∵PA⊥⊙O所在平面,
∴PA⊥⊙O所在平面内的所有直线,
∴PA⊥AC,PA⊥AB,PA⊥BC,
∴BC⊥面PAC,
∴BC⊥PC,
∵F是点A在PC上的射影,
∴AF⊥PC,
∵AF∩PC=F,
∴PC⊥面PAC,
∴AF⊥BC,
又AF⊥PC,
∴AF⊥面PBC,
∴AF⊥PB,∴①正确;
∵AF⊥面PBC,
BC?面PBC,
∴AF⊥BC∴③正确.
∵AF⊥PB,AE⊥PB,AF∩AE=A,
∴PB⊥面AEF,
∴EF⊥PB,
∴②正确.
∵AF⊥面PBC,
∴若AE⊥BC,
则AE⊥面PBC,
此时E,F重合,与已知矛盾.∴④错误;
故命题①②③正确,
故选:C
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面垂直的性质,考查化归与转化的数学思想方法.

练习册系列答案
相关题目
从不同号码的三双靴中任取4只,其中恰好有一双的取法种数为( )
| A、12 | B、24 | C、36 | D、72 |
812014除以100的余数是( )
| A、1 | B、79 | C、21 | D、81 |
在极坐标系中,过点A(1,0)且垂直于极轴的直线的极坐标方程为( )
| A、ρ=sinθ |
| B、ρ=1 |
| C、ρcosθ=1 |
| D、ρsinθ=1 |
如图,正方体ABCD-A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( )

| A、120° | B、90° |
| C、60° | D、30° |
设集合P={x∈R|x2+2x<0},Q={x∈R|
>0},则P∩Q=( )
| 1 |
| x+1 |
| A、(-2,1) | B、(-1,0) |
| C、∅ | D、(-2,0) |
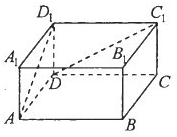 如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )
如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
双曲线
-
=1的渐近线方程是( )
| y2 |
| 9 |
| x2 |
| 16 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|