题目内容
在极坐标系中，过点A（1，0）且垂直于极轴的直线的极坐标方程为（ ）
| A、ρ=sinθ |
| B、ρ=1 |
| C、ρcosθ=1 |
| D、ρsinθ=1 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：设点P（x，y）是所求的直线上的任意一点，∠AOP=θ．利用直角三角形的边角关系可得
=cosθ，即可得出．
| OA |
| OP |
解答：
解：如图所示，
设点P（x，y）是所求的直线上的任意一点，∠AOP=θ．
则
=cosθ，∴ρcosθ=1．
故选：C．
设点P（x，y）是所求的直线上的任意一点，∠AOP=θ．
则
| OA |
| OP |
故选：C．
点评：本题考查了极坐标方程、直角三角形的边角关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}的通项公式an=-2n2+15n+2，则此数列的最大项是（ ）
| A、第1项 | B、第3项 |
| C、第4项 | D、第7项 |
如图，正方形ACDE与等腰直角三角形ACB所在的平面互相垂直，且AC=BC=2，∠ACB=90°，F，G分别是线段AE，BC的中点，则AD与GF所成的角的余弦值为（ ）A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
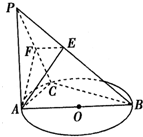如图，PA垂直于圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC，
正确命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
如果cosα=
有意义，那么m的取值范围是（ ）
| m+4 | ||
4
|
| A、m＜4 | B、m=4 |
| C、m＞4 | D、m≠4 |
已知双曲线
-
=1（a＞0，b＞0）左，右焦点分别为F1、F2．若在双曲线右支上存在一点P使|PF1|=4|PF2|，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（1，
| ||
| B、（1，2] | ||
C、[
| ||
D、[
|
已知空间四边形OABC各边及对角线长都相等，E，F分别为AB，OC的中点，则异面直线OE与BF所成角的余弦值为（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|