题目内容
如图,正方体ABCD-A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( )

| A、120° | B、90° |
| C、60° | D、30° |
考点:异面直线及其所成的角
专题:空间角
分析:以D为原点,建立空间直线坐标系D-xyz,利用向量法能求出异面直线GB与B′E所成的角.
解答:
解:以D为原点,建立如图所示的空间直线坐标系D-xyz,
设正方体ABCD-A′B′C′D′的棱长为2,
则G(0,0,1),B(2,2,0),B′(2,2,2),E(1,2,0),
∴
=(2,2,-1),
=(-1,0,-2),
∵
•
=-2+0+2=0,
∴
⊥
,
∴异面直线GB与B′E所成的角为90°.
故选:B.

设正方体ABCD-A′B′C′D′的棱长为2,
则G(0,0,1),B(2,2,0),B′(2,2,2),E(1,2,0),
∴
| GB |
| B′E |
∵
| GB |
| B′E |
∴
| GB |
| B′E |
∴异面直线GB与B′E所成的角为90°.
故选:B.
点评:本题考查异面直线所成的角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
下列四个函数中,能在x=0处取得极值的是( )
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x.
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x.
| A、①② | B、②③ | C、③④ | D、①③ |
若△ABC三内角A、B、C成等差数列,则∠B=60°的推理过程是( )
| A、归纳推理 | B、类比推理 |
| C、演绎推理 | D、合情推理 |
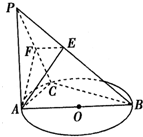 如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC,
正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
a=sin
,b=cos
,c=tan
,则a,b,c的大小关系是( )
| 2π |
| 5 |
| 5π |
| 6 |
| 7π |
| 5 |
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、a>c>b |
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离小于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f(x)=
,若方程f(x)=ax恰有两个不同的实根时,则实数a的取值范围是( )
|
| A、(0,e) | ||
B、(
| ||
| C、(e,4] | ||
| D、(0,4) |
复数z=
的共轭复数在复平面内对应的点在( )
| 1+2i2015 |
| 1-i2015 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |