题目内容
曲线y=x3在点P（-2，-8）处的切线方程是 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用,直线与圆
分析：求出函数的导数，求得曲线在点P处的切线的斜率，再由点斜式方程，即可得到切线方程．
解答：
解：y=x3在的导数为y′=3x2，
则曲线在点P（-2，-8）处的切线斜率为3×（-2）2=12，
即有曲线在点P（-2，-8）处的切线方程为y+8=12（x+2），
即为12x-y+16=0．
故答案为：12x-y+16=0．
则曲线在点P（-2，-8）处的切线斜率为3×（-2）2=12，
即有曲线在点P（-2，-8）处的切线方程为y+8=12（x+2），
即为12x-y+16=0．
故答案为：12x-y+16=0．
点评：本题考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，考查直线方程的形式，属于基础题．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
关于幂函数f（x）=x3，若0＜x1＜x2，则f（
）、
的大小关系（ ）
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
A、f（
| ||||
B、f（
| ||||
C、f（
| ||||
| D、无法确定 |
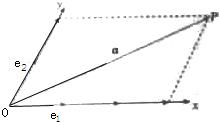如图，设Ox、Oy是平面内相交成60°角的两条数轴，
如图，有边长为1的正方形，取其对角线的一半，构成新的正方形，再取新正方形的对角线的一半，构成正方形…如此形成一个边长不断缩小的正方形系列．