题目内容
 如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.
如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.(1)求这一系列正方形的面积所构成的数列,并证明它是一个等比数列;
(2)从原始的正方形开始,到第9次构成新正方形时,共有10个正方形,求这10个正方形面积的和.
考点:等比数列的性质,数列的应用
专题:计算题,等差数列与等比数列
分析:(1)确定M1=1,M2=(
)2=
,…,Mn=(
)n-1,可得数列是一个等比数列;
(2)利用等比数列的求和公式,即可求这10个正方形面积的和.
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用等比数列的求和公式,即可求这10个正方形面积的和.
解答:
解:(1)设原正方形面积为M1,新的正方形面积依次为M1,M2,…,
易知:M1=1,M2=(
)2=
,…,Mn=(
)n-1,
∴数列是一个等比数列.
(2)M1+M2+…+M10=
=2[1-(
)10].
易知:M1=1,M2=(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴数列是一个等比数列.
(2)M1+M2+…+M10=
1•[1-(
| ||
1-
|
| 1 |
| 2 |
点评:本题考查等比数列的判断与求和,考查学生分析解决问题的能力,确定数列是等比数列是关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
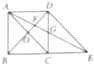 对于向量
对于向量| PAi |
| PA1 |
| PA2 |
| PAn |
| A、点A,C的“平衡点”必为点O |
| B、点D,C,E的“平衡点”为线段DE的中点 |
| C、点A,F,G,E的“平衡点”存在且唯一 |
| D、点A,B,E,D的“平衡点”必在点F |
 已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )
已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )| A、an=2n+1 |
| B、an=3n |
| C、an=4n-1 |
| D、an=2n-1 |
函数f(x)=
的图象大致是图中的( )
| cos(πx) |
| x2 |
A、 |
B、 |
C、 |
D、 |
