题目内容
已知某几何体的三视图(单位:cm)如图所示,则该几何体的表面积为 cm3.


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据三视图判断几何体是正方体削去一个三棱锥,截面三角形为等边三角形,根据正方体的边长计算截面三角形的边长,求出截面的面积,再求几何体的其他各面的面积,然后相加.
解答:
解:由三视图知几何体是边长为2的正方体削去一个三棱锥,其直观图如图:

截面三角形为等边三角形,边长为2
,
∴截面的面积为
×2
×2
×
=2
,
∴几何体的表面积S=3×2×2+3×
×2×2+2
=18+2
(cm2).
同理对面切去同样的三棱锥,几何体的表面积为S=2×2
+6×
×2×2=12+4
(cm2).
故答案为:18+2
或12+4
.

截面三角形为等边三角形,边长为2
| 2 |
∴截面的面积为
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
∴几何体的表面积S=3×2×2+3×
| 1 |
| 2 |
| 3 |
| 3 |
同理对面切去同样的三棱锥,几何体的表面积为S=2×2
| 3 |
| 1 |
| 2 |
| 3 |
故答案为:18+2
| 3 |
| 3 |
点评:本题考查了由三视图求几何体的表面积,解答此类问题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
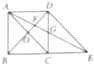 对于向量
对于向量| PAi |
| PA1 |
| PA2 |
| PAn |
| A、点A,C的“平衡点”必为点O |
| B、点D,C,E的“平衡点”为线段DE的中点 |
| C、点A,F,G,E的“平衡点”存在且唯一 |
| D、点A,B,E,D的“平衡点”必在点F |
