题目内容
同时抛掷三枚均匀的硬币，一枚反面朝上，二枚正面朝上的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：根据题意利用乘法原理可得：基本事件数8个，可求得出现一枚反面，二枚正面的有3种情形，从而求得概率．
解答：
解：抛掷三枚均匀的硬币，共出现2×2×2种情形，
出现一枚反面，二枚正面的有：C31=3，
∴出现一枚反面，二枚正面的概率是：
．
故选：C．
出现一枚反面，二枚正面的有：C31=3，
∴出现一枚反面，二枚正面的概率是：
| 3 |
| 8 |
故选：C．
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
相关题目
下表是甲、乙两个班级进行数学考试，按学生考试及格及不及格统计成绩后的2×2列联表：则X2的值为（ ）
| 不及格 | 及格 | 合计 | |
| 甲班 | 12 | 33 | 45 |
| 乙班 | 9 | 36 | 45 |
| 合计 | 21 | 69 | 90 |
| A、0.559 | B、0.456 |
| C、0.443 | D、0.4 |
将正方形ABCD沿对角线BD折成一个直二面角，点C到达点C1，则异面直线AB与C1D所成角是（ ）
| A、90° | B、60° |
| C、45° | D、30° |
当x∈[1，2]时，函数f（x）=ax2+4（a+1）x-3在x=2时取得最大值，则实数a的取值范围是（ ）
A、[-
| ||
| B、[0，+∞） | ||
| C、[1，+∞） | ||
D、[
|
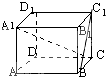如图，长方体ABCD-A1B1C1D1中，AB=AA1=2BC，则直线BC1与直线A1C所成角的余弦值为（ ）A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
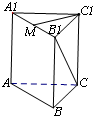如图，在直三棱柱ABC-A1B1C1的底面ABC中，CA=CB=1，∠BCA=90°，AA1=2，点M是A1B1的中点，则异面直线C1M与B1C所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对于数25，规定第1次操作为23+53=133，第2次操作为13+33+33=55，如此反复操作，则第100次操作后得到的数是（ ）
| A、25 | B、250 |
| C、55 | D、133 |
已知f（x+1）为偶函数，且f（x）在（-∞，1）单调递增，a=f（sin
），b=f（log53），c=f（tan
）则有（ ）
| π |
| 6 |
| π |
| 3 |
| A、a＜b＜c |
| B、b＜c＜a |
| C、c＜b＜a |
| D、c＜a＜b |