题目内容
已知函数f(x)为偶函数,且当x≥0时,f(x)=x2-2x.
(1)试比较f(-4)与f(2)的大小;
(2)求不等式
<0的解集.
(1)试比较f(-4)与f(2)的大小;
(2)求不等式
| f(x) |
| x |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据题意求出f(-4)=f(4)=8,f(2)=0,比较即可.(2)转化
或
求解即可.
|
|
解答:
解:(1)∵函数f(x)为偶函数,且当x≥0时,f(x)=x2-2x.
∴f(-4)=f(4)=8,f(2)=0,
∴f(-4)>f(2),
(2)∵当x≥0时,f(x)=x2-2x.
∴x<0,-x>0,
f(x)=f(-x)=x2+2x,(x<0)
∵不等式
<0,
∴
或
,
即0<x<2或x<-2,
不等式
<0的解集为:(0,2)∪(-∞,-2)
∴f(-4)=f(4)=8,f(2)=0,
∴f(-4)>f(2),
(2)∵当x≥0时,f(x)=x2-2x.
∴x<0,-x>0,
f(x)=f(-x)=x2+2x,(x<0)
∵不等式
| f(x) |
| x |
∴
|
|
即0<x<2或x<-2,
不等式
| f(x) |
| x |
点评:本题考查了函数的性质,不等式的解法,属于中档题,运用转化思想.

练习册系列答案
相关题目
 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.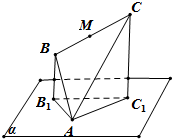 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是