题目内容
已知A(-2,0),B(2,0),点P在圆(x-3)2+(y-4)2=1上运动,则PA2+PB2的最小值是 .
考点:两点间距离公式的应用
专题:计算题,直线与圆
分析:由点A(-2,0),B(2,0),设P(a,b),则|PA|2+|PB|2=2a2+2b2+8,由点P在圆(x-3)2+(y-4)2=1上运动,通过三角代换,化简|PA|2+|PB|2为一个角的三角函数的形式,然后求出最小值.
解答:
解:∵点A(-2,0),B(2,0),
设P(a,b),则|PA|2+|PB|2=2a2+2b2+8,
由点P在圆(x-3)2+(y-4)2=1上运动,
(a-3)2+(b-4)2=1,
令a=3+cosα,b=4+sinα,
所以|PA|2+|PB|2=2a2+2b2+8
=2(3+cosα)2+2(4+sinα)2+8
=60+12cosα+16sinα
=60+20sin(α+φ),(tanφ=
).
所以|PA|2+|PB|2≥40.当且仅当sin(α+φ)=-1时,取得最小值.
∴|PA|2+|PB|2的最小值为40.
故答案为:40.
设P(a,b),则|PA|2+|PB|2=2a2+2b2+8,
由点P在圆(x-3)2+(y-4)2=1上运动,
(a-3)2+(b-4)2=1,
令a=3+cosα,b=4+sinα,
所以|PA|2+|PB|2=2a2+2b2+8
=2(3+cosα)2+2(4+sinα)2+8
=60+12cosα+16sinα
=60+20sin(α+φ),(tanφ=
| 3 |
| 4 |
所以|PA|2+|PB|2≥40.当且仅当sin(α+φ)=-1时,取得最小值.
∴|PA|2+|PB|2的最小值为40.
故答案为:40.
点评:本题考查直线的一般式方程与两点间距离公式的应用,具体涉及到直线方程和圆的简单性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
已知三棱锥的三视图如图所示,则它的外接球的表面积为( )


| A、4π | B、8π |
| C、12π | D、16π |
已知圆x2+y2=4与圆x2+y2-2y-6=0,则两圆的公共弦长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
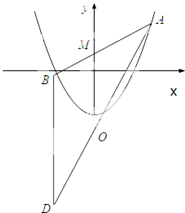 如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).