题目内容
解方程:3×3x+2=32x+3.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:令 t=3x>0,可得27t2-3t-2=0,求得t的值,可得x的值.
解答:
解:方程即 3•3x+2=27•32x,令 t=3x>0,可得27t2-3t-2=0,
求得t=
,或t=-
(舍去),即 3x=
,∴x=-1.
求得t=
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
点评:本题主要考查一元二次方程的解法,指数函数的值域,体现了转化的数学思想,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
集合M={-2,0,1,2},N={x|x2-x>0},则M∩N=( )
| A、{-2,1,2} |
| B、{0,2} |
| C、{-2,2} |
| D、[-2,2] |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.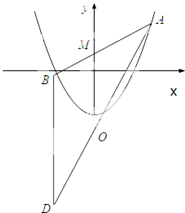 如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).