题目内容
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分必要条件定义判断,结合不等式求解.
解答:
解:∵a,b∈R,则(a-b)a2<0,
∴a<b成立,
由a<b,则a-b<0,“(a-b)a2≤0,
所以根据充分必要条件的定义可的判断:
a,b∈R,则“(a-b)a2<0”是a<b的充分不必要条件,
故选:A
∴a<b成立,
由a<b,则a-b<0,“(a-b)a2≤0,
所以根据充分必要条件的定义可的判断:
a,b∈R,则“(a-b)a2<0”是a<b的充分不必要条件,
故选:A
点评:本题考查了不等式,充分必要条件的定义,属于容易题.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )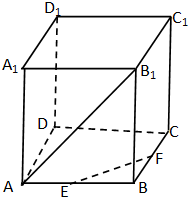

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式组
,表示的平面区域的面积为( )
|
| A、4 | B、1 | C、5 | D、无穷大 |