题目内容
已知二次函数f(x)=x2+bx+c的图象经过点(1,-2)和点(3,2).
(1)求f(x)的表达式;
(2)当x∈[2,3]时,求f(x)的值域.
(1)求f(x)的表达式;
(2)当x∈[2,3]时,求f(x)的值域.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)代入点(1,-2)和点(3,2),得到b,c的方程组,解得即可;
(2)求得对称轴,判断区间与对称轴的关系,运用单调性,即可得到值域.
(2)求得对称轴,判断区间与对称轴的关系,运用单调性,即可得到值域.
解答:
解:(1)f(x)=x2+bx+c,
代入点(1,-2)和点(3,2),
得
,解得
,
则f(x)=x2-2x-1;
(2)f(x)的对称轴为x=1,
则f(x)在[2,3]上为增函数,
f(2)=4-4-1=-1,f(3)=9-6-1=2,
则f(x)的值域为[-1,2].
代入点(1,-2)和点(3,2),
得
|
|
则f(x)=x2-2x-1;
(2)f(x)的对称轴为x=1,
则f(x)在[2,3]上为增函数,
f(2)=4-4-1=-1,f(3)=9-6-1=2,
则f(x)的值域为[-1,2].
点评:本题考查二次函数的解析式的求法,考查二次函数的值域求法,注意运用单调性,属于基础题.

练习册系列答案
相关题目
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
对任意两实数a、b,定义运算“*”如下:a*b=
,则函数f(x)=(log
x)*log2x的值域为( )
|
| 1 |
| 2 |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、[0,+∞) |
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
|
| A、(0,2016) |
| B、(0,2016] |
| C、(0,504) |
| D、(0,504] |
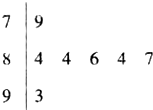 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |
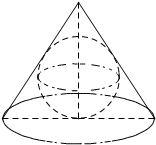 一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=
一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=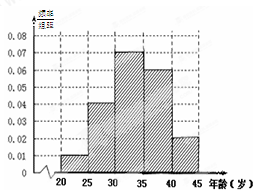 上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.根据如图所示的频率分布直方图,估计这507个画师中年龄不超过30岁的人数约
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.根据如图所示的频率分布直方图,估计这507个画师中年龄不超过30岁的人数约