题目内容
设函数f(x)=kx2-4kx+2在[-4,3]上有最大值3,试求常数k的值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:先用配方法将函数变形,求出其对称轴,再根据开口方向,确定函数的单调性,明确取最大值的状态,再计算.
解答:
解:∵f(x)=kx2-4kx+2=k(x-2)2-4k+2,∴对称轴为x=2,
(1)当k>0时,二次函数图象开口向上,
当x=-4时,f(x)有最大值,f(-4)=k•(-4)2-4k×(-4)+2=32k=3
∴k=
;
(2)当k<0时,二次函数图象开口向下,
当x=2时,f(x)有最大值,f(2)=-4k+2=3
∴k=-
.
(3)当k=0时,显然不成立.
故k的取值集合为:{
,-
}.
(1)当k>0时,二次函数图象开口向上,
当x=-4时,f(x)有最大值,f(-4)=k•(-4)2-4k×(-4)+2=32k=3
∴k=
| 3 |
| 32 |
(2)当k<0时,二次函数图象开口向下,
当x=2时,f(x)有最大值,f(2)=-4k+2=3
∴k=-
| 1 |
| 4 |
(3)当k=0时,显然不成立.
故k的取值集合为:{
| 3 |
| 32 |
| 1 |
| 4 |
点评:本题主要考查函数最值的求法,基本思路是:二次项系数位置有参数时,先分类讨论,再确定对称轴和开口方向,明确单调性,再研究函数最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
给出下列四个命题:其中真命题的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
数列{an}是各项均为正数的等比数列,公比q=3且a1a2a3…a30=330,则a3a6a9…a30=( )
| A、310 |
| B、315 |
| C、320 |
| D、325 |
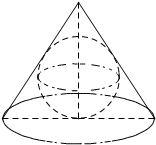 一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=
一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=