题目内容
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )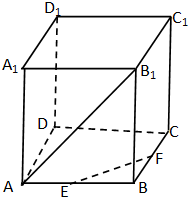

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:先通过平移将两条异面直线平移到同一个起点A,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.
解答:
解:如图,将EF平移到AC,连结B1C,
则∠B1AC为异面直线AB1与EF所成的角,
∵三角形B1AC为等边三角形,
∴故异面直线AB1与EF所成的角60°,
∴cos∠B1AC=
.
故选A.
则∠B1AC为异面直线AB1与EF所成的角,
∵三角形B1AC为等边三角形,
∴故异面直线AB1与EF所成的角60°,
∴cos∠B1AC=
| 1 |
| 2 |
故选A.
点评:本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
数列{an}是各项均为正数的等比数列,公比q=3且a1a2a3…a30=330,则a3a6a9…a30=( )
| A、310 |
| B、315 |
| C、320 |
| D、325 |
对任意两实数a、b,定义运算“*”如下:a*b=
,则函数f(x)=(log
x)*log2x的值域为( )
|
| 1 |
| 2 |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、[0,+∞) |
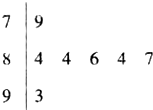 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |