Question

不等式组

2x+y-6≤0 x+y-3≥0 y≤2

，表示的平面区域的面积为（　　）

• A、4
• B、1
• C、5
• D、无穷大

Answer 1

考点：二元一次不等式（组）与平面区域

专题：不等式的解法及应用

分析：画出不等式组

2x+y-6≤0 x+y-3≥0 y≤2

表示的平面区域为三角形ABC及其内部的部分，求得A、B、C各个点的坐标，可得三角形ABC的面积．

解答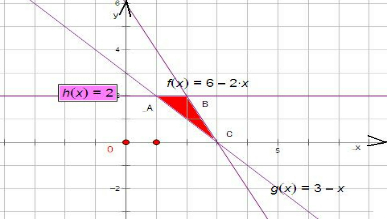： 解：不等式组

2x+y-6≤0 x+y-3≥0 y≤2

表示的平面区域为三角形ABC及其内部的部分，如图所示：容易求得A（1，2），B（2，2），C（3，0），
不等式组

2x+y-6≤0 x+y-3≥0 y≤2

表示的平面区域的面积是三角形ABC的面积，结合图形易求|AB|=1，C到AB的距离d=2，
故S_△ABC=

1

2

×|AB|×d=

1

2

×1×2=1．
故选：B．

点评：本题主要考查二元一次不等式组表示平面区域，体现了数形结合的数学思想，属于基础题．