题目内容
化简：cos（kπ+a）+cos（kπ-a）（k∈Z）．
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：对整数k分奇偶讨论，利用诱导公式化简即可．
解答：
解：当k=2m（m∈Z）时，
cos（kπ+a）+cos（kπ-a）
=cos（2mπ+a）+cos（2mπ-a）
=cosa+cosa=2cosa；
当k=2m+1（m∈Z）时，
原式=cos（2mπ+π+a）+cos（2mπ+π-a）
=-cosa-cosa
=-2cosa；
∴cos（kπ+a）+cos（kπ-a）=
．
cos（kπ+a）+cos（kπ-a）
=cos（2mπ+a）+cos（2mπ-a）
=cosa+cosa=2cosa；
当k=2m+1（m∈Z）时，
原式=cos（2mπ+π+a）+cos（2mπ+π-a）
=-cosa-cosa
=-2cosa；
∴cos（kπ+a）+cos（kπ-a）=
|
点评：本题考查三角函数的化简求值，考查诱导公式的应用，对k（k∈Z）分类讨论是关键，属于中档题．
练习册系列答案
相关题目
在△ABC中，AB=1，BC=2，
•
=
，则角B=（ ）
| BA |
| BC |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
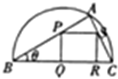如图所示，在直径为BC的半圆中，A是弧BC上一点，正方形PQRS内接于△ABC，若BC=a，∠ABC=θ，设△ABC的面积为Sl，正方形PQRS的面积为S2．