题目内容
已知f（x）=
是定义域R上的减函数，则a的取值范围是 ．
|
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据分段函数的单调性的性质建立条件关系，即可求出a的取值范围．
解答：
解：要使函数f（x）是减函数，
则当x＜1时，满足函数递减，即此时3a-4＜0，此时a＜
，
当x≥1时，函数满足单调递减，此时
，
即
，∴a≥1，
要使f（x）是定义域R上的减函数，
则3a-4+4a≥-a+2+3，
即a≥
，
综上：
，
即
≤a＜
，
故答案为：
≤a＜
．
则当x＜1时，满足函数递减，即此时3a-4＜0，此时a＜
| 4 |
| 3 |
当x≥1时，函数满足单调递减，此时
|
即
|
要使f（x）是定义域R上的减函数，
则3a-4+4a≥-a+2+3，
即a≥
| 9 |
| 8 |
综上：
|
即
| 9 |
| 8 |
| 4 |
| 3 |
故答案为：
| 9 |
| 8 |
| 4 |
| 3 |
点评：本题主要考查分段函数的单调性的应用，要求熟练掌握分段函数单调性的性质．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
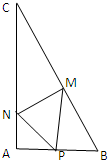在Rt△ABC中，AB=2，AC=4，∠A为直角，P为AB中点，M、N分别是BC，AC上任一点，则△MNP周长的最小值是集合A={0，1，2，3，4}，B={x|x2-x＞0}，则A∩B=（ ）
| A、{2，3，4} |
| B、{1} |
| C、{x|2＜x≤4} |
| D、{x|x＜0或x＞2} |