题目内容
设θ为第三象限角，试判断cos
的符号．
| θ |
| 3 |
考点：三角函数值的符号
专题：三角函数的求值
分析：写出第三象限角的范围，得到
的范围，然后分类讨论得到cos
的符号．
| θ |
| 3 |
| θ |
| 3 |
解答：
解：∵θ为第三象限角，∴2kπ-π＜θ＜2kπ-
，k∈Z，
则
-
＜
＜
-
，k∈Z．
当k=3n，n∈Z时，2nπ-
＜
＜2nπ-
，cos
＞0；
当k=3n+1，n∈Z时，2nπ+
＜
＜2nπ+
，cos
＞0；
当k=3n+2，2nπ+π＜
＜2nπ+
，cos
＜0．
| π |
| 2 |
则
| 2kπ |
| 3 |
| π |
| 3 |
| θ |
| 3 |
| 2kπ |
| 3 |
| π |
| 6 |
当k=3n，n∈Z时，2nπ-
| π |
| 3 |
| θ |
| 3 |
| π |
| 6 |
| θ |
| 3 |
当k=3n+1，n∈Z时，2nπ+
| π |
| 3 |
| θ |
| 3 |
| π |
| 2 |
| θ |
| 3 |
当k=3n+2，2nπ+π＜
| θ |
| 3 |
| 7π |
| 6 |
| θ |
| 3 |
点评：本题考查了象限角及象限符号，体现了分类讨论的数学思想方法，是基础题．
练习册系列答案
53随堂测系列答案
相关题目
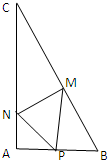在Rt△ABC中，AB=2，AC=4，∠A为直角，P为AB中点，M、N分别是BC，AC上任一点，则△MNP周长的最小值是