题目内容
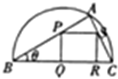 如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.
如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求
| S1 |
| S2 |
考点:三角函数的最值,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)根据AB=acosθ,AC=asinθ,可得S1=
•AB•AC的值.设正方形边长为x,BQ=x•cotθ,RC=x•tanθ,
则由BC=x+x•cotθ+x•tan θ=a,解得x的值,可得S2=x2 的值.
(2)根据
=
sin2θ+
+1,设sin 2θ=t,则y=
=
(t+
+4),由于f(t)=t+
(0<t≤1),以及f(t)在(0,1]上是减函数,可得
取最小值,以及此时的θ值.
| 1 |
| 2 |
则由BC=x+x•cotθ+x•tan θ=a,解得x的值,可得S2=x2 的值.
(2)根据
| S1 |
| S2 |
| 1 |
| 4 |
| 1 |
| sin2θ |
| S1 |
| S2 |
| 1 |
| 4 |
| 4 |
| t |
| 4 |
| t |
| S1 |
| S2 |
解答:
解:(1)因为AB=acosθ,AC=asinθ,∴S1=
•AB•AC=
a•cosθ•asinθ=
a2sin 2θ.
设正方形边长为x,BQ=x•cotθ,RC=x•tanθ,
则x+x•cotθ+x•tan θ=a,解得x=
,
所以S2=x2=
.
(2)当a固定,θ变化时,
=
=
+
+1
=
sin2θ+
+1,
设sin 2θ=t,则y=
=
(t+
+4),
∵0<t≤1,f(t)=t+
(0<t≤1),
易证f(t)在(0,1]上是减函数.
故当t=1时,f(t)取得最小值,此时,
取最小值,此时,2θ=
,θ=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
设正方形边长为x,BQ=x•cotθ,RC=x•tanθ,
则x+x•cotθ+x•tan θ=a,解得x=
| a•sinθcosθ |
| sinθcosθ+1 |
所以S2=x2=
| a2•sin2θ•cos 2θ |
| sin2θcos 2θ+1+2sinθcosθ |
(2)当a固定,θ变化时,
| S1 |
| S2 |
| sin2θ•cos 2θ+1+2sinθcosθ |
| 2sinθcosθ |
| sinθcosθ |
| 2 |
| 1 |
| 2sinθcosθ |
=
| 1 |
| 4 |
| 1 |
| sin2θ |
设sin 2θ=t,则y=
| S1 |
| S2 |
| 1 |
| 4 |
| 4 |
| t |
∵0<t≤1,f(t)=t+
| 4 |
| t |
易证f(t)在(0,1]上是减函数.
故当t=1时,f(t)取得最小值,此时,
| S1 |
| S2 |
| π |
| 2 |
| π |
| 4 |
点评:本题主要考查直角三角形中的边角关系,利用函数的单调性求函数的最值,属于中档题.

练习册系列答案
相关题目
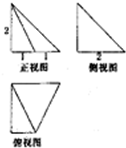 某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )
某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )| A、1 | B、2 | C、3 | D、4 |