题目内容
已知
=（cosα，sinα），
=（2sinβ，2cosβ），且|2k
+
|=
|2
-k
|（k＞0），设
与
的夹角为θ．
（1）求cosθ与k的函数关系式；
（2）当θ取最大值时，求α，β满足的关系式．
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
（1）求cosθ与k的函数关系式；
（2）当θ取最大值时，求α，β满足的关系式．
考点：三角函数中的恒等变换应用,平面向量数量积的坐标表示、模、夹角
专题：计算题,平面向量及应用
分析：（1）依题意，将等式|2k
+
|=
|2
-k
|（k＞0）两边平方，利用向量的数量积，整理可得k2-4kcosθ+1=0，从而可得cosθ与k的函数关系式；
（2）由（1）知cosθ=
（k+
）（k＞0），利用基本不等式可求得cosθ=
（k+
）≥
，又θ∈[0，π]，可求得θ的最大值，继而可得α，β满足的关系式．
| a |
| b |
| 3 |
| a |
| b |
（2）由（1）知cosθ=
| 1 |
| 4 |
| 1 |
| k |
| 1 |
| 4 |
| 1 |
| k |
| 1 |
| 2 |
解答：
解：（1）∵|2k
+
|=
|2
-k
|（k＞0），
∴等式两边平方，
得：4k2
2+4k
•
+
2=3（4
2-4k
•
+k2
2），
∵
=（cosα，sinα），
=（2sinβ，2cosβ），
∴
2=1，
2=4，又＜
，
＞=θ，
∴4k2+4k×1×2cosθ+4=12-12k×1×2cosθ+12k2，
整理得，k2-4kcosθ+1=0，
∴cosθ=
（k+
）（k＞0）；
（2）由（1）知，k＞0，cosθ=
（k+
）≥
，又θ∈[0，π]，
∴0≤θ≤
，
∴θmax=
，
∴当θ取最大值
时，
=（
，
），
=（
，1），
∴
•
=
×
+
×1=
，
又
•
=2cosαsinβ+2sinαcosβ=2sin（α+β），
∴2sin（α+β）=
，
∴sin（α+β）=
，
∴α+β=2nπ+
，或α+β=2nπ+
（n∈Z）．
| a |
| b |
| 3 |
| a |
| b |
∴等式两边平方，
得：4k2
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
∵
| a |
| b |
∴
| a |
| b |
| a |
| b |
∴4k2+4k×1×2cosθ+4=12-12k×1×2cosθ+12k2，
整理得，k2-4kcosθ+1=0，
∴cosθ=
| 1 |
| 4 |
| 1 |
| k |
（2）由（1）知，k＞0，cosθ=
| 1 |
| 4 |
| 1 |
| k |
| 1 |
| 2 |
∴0≤θ≤
| π |
| 3 |
∴θmax=
| π |
| 3 |
∴当θ取最大值
| π |
| 3 |
| a |
| 1 |
| 2 |
| ||
| 2 |
| b |
| 3 |
∴
| a |
| b |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
又
| a |
| b |
∴2sin（α+β）=
| 3 |
∴sin（α+β）=
| ||
| 2 |
∴α+β=2nπ+
| π |
| 3 |
| 2π |
| 3 |
点评：本题考查平面向量数量积的坐标表示及夹角，考查基本不等式及两角和的正弦，考查等价转化思想与综合运算能力，属于难题．
练习册系列答案
相关题目
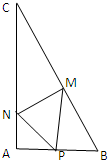在Rt△ABC中，AB=2，AC=4，∠A为直角，P为AB中点，M、N分别是BC，AC上任一点，则△MNP周长的最小值是