题目内容
已知函数f(x)=2x2-2ax+b,当时x=-1时,f(x)取最小值-8,记集合A={x|f(x)>0},B={x||x-t|≤1}
(Ⅰ)当t=1时,求(∁RA)∪B;
(Ⅱ)设命题P:A∩B≠∅,若¬P为真命题,求实数t的取值范围.
(Ⅰ)当t=1时,求(∁RA)∪B;
(Ⅱ)设命题P:A∩B≠∅,若¬P为真命题,求实数t的取值范围.
考点:命题的否定,二次函数的性质
专题:函数的性质及应用,简易逻辑
分析:(I)根据题意求出f(x)的解析式,再求出集合A以及t=1时的集合B,即可求出答案;
(Ⅱ)根据命题与命题的否定一真一假,得出命题P是假命题,从而列出不等式组,求出解集.
(Ⅱ)根据命题与命题的否定一真一假,得出命题P是假命题,从而列出不等式组,求出解集.
解答:
解:(Ⅰ)∵函数f(x)=2x2-2ax+b,
在x=-1时,f(x)取最小值-8,
∴
;
解得a=-2,b=-6,
∴f(x)=2x2+4x-6;
∴集合A={x|f(x)>0}={x|2x2+4x-6>0}={x|x<-3,或x>1},
∴CRA={x|-3≤x≤1};
当t=1时,B={x||x-1|≤1}={x|0≤x≤2},
∴(∁RA)∪B={x|-3≤x≤2};
(Ⅱ)∵B={x||x-t|≤1}={x|t-1≤x≤t+1},
由题意知命题P:A∩B≠∅为假命题,
∴
,
解得-2≤t≤0;
∴实数t的取值范围是[-2,0].
在x=-1时,f(x)取最小值-8,
∴
|
解得a=-2,b=-6,
∴f(x)=2x2+4x-6;
∴集合A={x|f(x)>0}={x|2x2+4x-6>0}={x|x<-3,或x>1},
∴CRA={x|-3≤x≤1};
当t=1时,B={x||x-1|≤1}={x|0≤x≤2},
∴(∁RA)∪B={x|-3≤x≤2};
(Ⅱ)∵B={x||x-t|≤1}={x|t-1≤x≤t+1},
由题意知命题P:A∩B≠∅为假命题,
∴
|
解得-2≤t≤0;
∴实数t的取值范围是[-2,0].
点评:本题考查了二次函数的图象与性质的应用问题,也考查了简易逻辑的应用问题以及集合的应用问题,是综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、10 | B、8 | C、3 | D、2 |
设
、
、
是任意的非零平面向量,且相互不共线,则
①(
•
)
=(
•
)
;
②|
|-|
|>|
-
|;
③(
•
)
-(
•
)
与
垂直;
④(3
+2
)•(3
-2
)=9|
|2-4|
|2中,是真命题的有( )
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
②|
| a |
| b |
| a |
| b |
③(
| b |
| c |
| a |
| c |
| a |
| b |
| c |
④(3
| a |
| b |
| a |
| b |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、②④ |
在钝角三角形ABC中,a=1,b=2,则最大边c的取值范围是( )
A、(
| ||
B、(
| ||
| C、(2,3) | ||
D、(
|
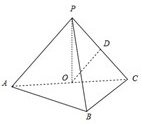 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.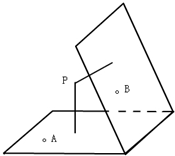 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为