题目内容
已知对称中心为坐标原点的椭圆C1与抛物线C2:x2=4y有一个相同的焦点F1,直线l:y=2x+m与抛物线C2只有一个公共点.
(Ⅰ)求直线l的方程;
(Ⅱ)若椭圆C1经过直线l上的点P,当椭圆C1的长轴长取最小值时,求椭圆C1的方程及点P的坐标.
(Ⅰ)求直线l的方程;
(Ⅱ)若椭圆C1经过直线l上的点P,当椭圆C1的长轴长取最小值时,求椭圆C1的方程及点P的坐标.
考点:直线与圆锥曲线的关系,直线的一般式方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)直接把直线方程和抛物线方程联立,利用判别式等于0求解m的值,代入后可得直线方程;
(Ⅱ)由抛物线的焦点坐标得到椭圆的两焦点坐标,求出点F1 关于直线l的对称点,然后利用三角形两边之和大于第三边得到使椭圆C1的长轴长取最小值时点P的坐标,并求得椭圆长轴的最小值,则答案可求.
(Ⅱ)由抛物线的焦点坐标得到椭圆的两焦点坐标,求出点F1 关于直线l的对称点,然后利用三角形两边之和大于第三边得到使椭圆C1的长轴长取最小值时点P的坐标,并求得椭圆长轴的最小值,则答案可求.
解答:
解:(Ⅰ)由
消去y,得x2-8x-4m=0.
∵直线l与抛物线C2只有一个公共点,
∴△=82+4×4m=0,解得m=-4.
∴直线l的方程为y=2x-4;
(Ⅱ)∵抛物线C2的焦点为:F1(0,1),
依题意知椭圆C1 的两个焦点坐标为F1(0,1),F2(0,-1),
如图,
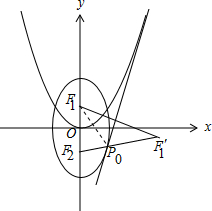
设点F1关于直线l的对称点为F1′(x0,y0),
则
,解得
.
∴点F1′(4,-1).
∴直线F1′F2 的方程为y=-1.
直线l与直线F1′F2 的交点坐标为P0(
,-1).
由椭圆的定义及平面几何知识得:
椭圆C1的长轴长2a=|PF1|+|PF2|=|PF1′|+|PF2|≥|F1′F2|=4.
其中当P与P0重合时上式取等号.
∴当a=2时,椭圆的长轴长取得最小值为4,
此时椭圆的方程为
+
=1,点P的坐标为(
,-1).
|
∵直线l与抛物线C2只有一个公共点,
∴△=82+4×4m=0,解得m=-4.
∴直线l的方程为y=2x-4;
(Ⅱ)∵抛物线C2的焦点为:F1(0,1),
依题意知椭圆C1 的两个焦点坐标为F1(0,1),F2(0,-1),
如图,

设点F1关于直线l的对称点为F1′(x0,y0),
则
|
|
∴点F1′(4,-1).
∴直线F1′F2 的方程为y=-1.
直线l与直线F1′F2 的交点坐标为P0(
| 3 |
| 2 |
由椭圆的定义及平面几何知识得:
椭圆C1的长轴长2a=|PF1|+|PF2|=|PF1′|+|PF2|≥|F1′F2|=4.
其中当P与P0重合时上式取等号.
∴当a=2时,椭圆的长轴长取得最小值为4,
此时椭圆的方程为
| y2 |
| 4 |
| x2 |
| 3 |
| 3 |
| 2 |
点评:本题是直线与圆锥曲线的综合题,考查了直线与圆锥曲线的关系,训练了利用三角形两边之和大于第三边求最值点,体现了数学转化思想方法,考查了椭圆方程的求法,是压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设偶函数f(x)=
sin(2x+φ)-cos(2x+φ)(|φ|<
),则( )
| 3 |
| π |
| 2 |
A、y=f(x)的对称中心为(
| ||||||
B、y=f(x)的对称中心为(
| ||||||
C、y=f(x)的对称中心为(
| ||||||
D、y=f(x)的对称中心为(
|
若函数f(x)=sin2x-
(x∈R),则f(x)是( )
| 1 |
| 2 |
A、最小正周期为
| ||
| B、最小正周期为π的奇函数 | ||
| C、最小正周期为2π的偶函数 | ||
| D、最小正周期为π的偶函数 |
下列命题中为假命题的是( )
| A、?x∈R,logax=-1(a>0,a≠1) |
| B、?x∈R,tanx=2014 |
| C、?x∈R,ax>0(a>0,a≠1) |
| D、?x∈R,x2+ax+a2>0(a∈R) |
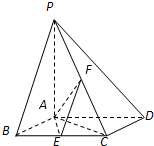 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.
在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.