题目内容
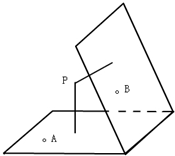 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为考点:与二面角有关的立体几何综合题
专题:计算题,空间角
分析:作出P关于两个平面α,β对称点M、N,连接MN,线段MN与两个平面的交点坐标分别为C,D,连接MP,NP,由已知条件推导出△PAB周长L=PM+PN+MN=AM+MN+BN,当A与C重合,B与D重合时,由两点之间线段最短可以得出MN,即为△PAB周长的最小值.
解答:
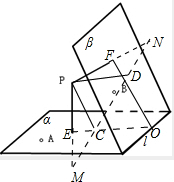 解:如图,作出P关于两个平面α,β的对称点M、N,连接MN,
解:如图,作出P关于两个平面α,β的对称点M、N,连接MN,
线段MN与两个平面的交点坐标分别为C,D,连接MP,NP,CP,DP,
则△PAB的周长L=PA+PB+AB=AM+AB+BN,当A与C重合,B与D重合时,
由两点之间线段最短可以得出MN即为△PAB周长的最小值,
根据题意可知:P到二面角两个面的距离分别为2、3,
∴MP=4,NP=6,
∵大小为60°的二面角α-l-β,
∴∠EOF=60°,
∴∠MPN=120°,
根据余弦定理有:
MN2=MP2+NP2-2MP•NP•cos∠MPN=42+62-2×4×6×(-
)=76,
∴MN=2
,
∴△PAB周长的最小值等于2
.
故答案为:2
.
 解:如图,作出P关于两个平面α,β的对称点M、N,连接MN,
解:如图,作出P关于两个平面α,β的对称点M、N,连接MN,线段MN与两个平面的交点坐标分别为C,D,连接MP,NP,CP,DP,
则△PAB的周长L=PA+PB+AB=AM+AB+BN,当A与C重合,B与D重合时,
由两点之间线段最短可以得出MN即为△PAB周长的最小值,
根据题意可知:P到二面角两个面的距离分别为2、3,
∴MP=4,NP=6,
∵大小为60°的二面角α-l-β,
∴∠EOF=60°,
∴∠MPN=120°,
根据余弦定理有:
MN2=MP2+NP2-2MP•NP•cos∠MPN=42+62-2×4×6×(-
| 1 |
| 2 |
∴MN=2
| 19 |
∴△PAB周长的最小值等于2
| 19 |
故答案为:2
| 19 |
点评:本题考查三角形周长的最小值的求法,注意运用对称的方法,同时考查二面角的定义和求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
| A、4倍 | ||
| B、3倍 | ||
C、
| ||
| D、2倍 |
(理做)已知函数f(x)=
-lnx,函数y=f(|x|)的零点个数为n,则n=( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |
下列式子正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、λ(μa)=(λμ)
| ||||||||||||
D、
|
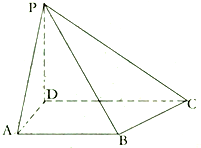 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD= (1)设x,y∈R,向量
(1)设x,y∈R,向量