题目内容
已知数列{an}中,a1=t(t为非零常数),{an}的前n项和Sn满足Sn+1=3Sn.
(Ⅰ)当t=1时,求数列{an}的通项公式;
(Ⅱ)若对任意n∈N*,都有λ>
,求实数λ的取值范围.
(Ⅰ)当t=1时,求数列{an}的通项公式;
(Ⅱ)若对任意n∈N*,都有λ>
| n(n+1) |
| an |
考点:数列递推式
专题:计算题,点列、递归数列与数学归纳法
分析:(Ⅰ)方法一:先求{Sn}的通项,再求数列{an}的通项公式;方法二:由Sn+1=3Sn,再写一式,两式相减,可得{an}为第二项起的等比数列,公比为3,即可求数列{an}的通项公式;
(Ⅱ)分类讨论,确定数列的通项及单调性,求最值,根据λ>
,即可求实数λ的取值范围.
(Ⅱ)分类讨论,确定数列的通项及单调性,求最值,根据λ>
| n(n+1) |
| an |
解答:
解:(Ⅰ)
方法一:由Sn+1=3Sn得:数列{Sn}是等比数列,公比为3,首项为1 …(2分)
∴Sn=1•3n-1=3n-1…(3分)
当n≥2时,an=Sn-Sn-1=3n-1-3n-2=2•3n-2…(4分)
∴an=
…(5分)
方法二:∵Sn+1=3Sn,∴Sn=3Sn-1(n≥2)
以上两式相减得:an+1=3an(n≥2),…(2分)
在Sn+1=3Sn中,取n=1得:a1+a2=3a1即a2=2a1=2,…(3分)
∴
=2≠3,
∴{an}为第二项起的等比数列,公比为3 …(4分)
∴an=
…(5分)
(Ⅱ)令bn=
由(Ⅰ)知:{an}为第二项起的等比数列,公比为3,a2=2t,
∴当n≥2时,an=2t•3n-2,bn=
…(6分)
∴bn+1-bn=
-
=
…(7分)
①若t>0,则bn+1-bn<0,即bn+1<bn(n≥2),
∴数列{bn}是从第二项起的递减数列…(8分)
而b1=
,b2=
,
∴b2>b1,
∴(bn)max=b2=
…(9分)
∵对任意n∈N*,都有λ>
,
∴λ>
…(10分)
②若t<0,则bn+1-bn>0,即bn+1>bn(n≥2),
∴数列{bn}是从第二项起的递增数列 …(11分)
而b1=
<0,当n≥2时,bn=
<0,
∴bn∈(-∞,0)…(12分)
∵对任意n∈N*,都有λ>
,∴λ≥0…(13分)
综合上面:若t>0,则λ>
;若t<0,则λ≥0. …(14分)
方法一:由Sn+1=3Sn得:数列{Sn}是等比数列,公比为3,首项为1 …(2分)
∴Sn=1•3n-1=3n-1…(3分)
当n≥2时,an=Sn-Sn-1=3n-1-3n-2=2•3n-2…(4分)
∴an=
|
方法二:∵Sn+1=3Sn,∴Sn=3Sn-1(n≥2)
以上两式相减得:an+1=3an(n≥2),…(2分)
在Sn+1=3Sn中,取n=1得:a1+a2=3a1即a2=2a1=2,…(3分)
∴
| a2 |
| a1 |
∴{an}为第二项起的等比数列,公比为3 …(4分)
∴an=
|
(Ⅱ)令bn=
| n(n+1) |
| an |
由(Ⅰ)知:{an}为第二项起的等比数列,公比为3,a2=2t,
∴当n≥2时,an=2t•3n-2,bn=
| n(n+1) |
| 2t•3n-2 |
∴bn+1-bn=
| (n+1)(n+2) |
| 2t•3n-1 |
| n(n+1) |
| 2t•3n-2 |
| (n+1)(1-n) |
| t•3n-1 |
①若t>0,则bn+1-bn<0,即bn+1<bn(n≥2),
∴数列{bn}是从第二项起的递减数列…(8分)
而b1=
| 2 |
| t |
| 3 |
| t |
∴b2>b1,
∴(bn)max=b2=
| 3 |
| t |
∵对任意n∈N*,都有λ>
| n(n+1) |
| an |
∴λ>
| 3 |
| t |
②若t<0,则bn+1-bn>0,即bn+1>bn(n≥2),
∴数列{bn}是从第二项起的递增数列 …(11分)
而b1=
| 2 |
| t |
| n(n+1) |
| 2t•3n-2 |
∴bn∈(-∞,0)…(12分)
∵对任意n∈N*,都有λ>
| n(n+1) |
| an |
综合上面:若t>0,则λ>
| 3 |
| t |
点评:本题考查数列的通项,考查数列的单调性,考查学生的计算能力,确定数列的通项是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线mx-y+2=0与圆x2+y2=1只有一个交点,则实数m的值是( )
| A、±1 | ||
B、±
| ||
C、±
| ||
| D、±2 |
在同一直角坐标系中,经过伸缩变换
后,曲线C变为曲线x′2+y′2=1,则曲线C的方程为( )
|
| A、25x2+9y2=1 | ||||
| B、9x2+25y2=1 | ||||
| C、25x+9y=1 | ||||
D、
|
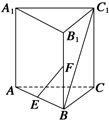 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1的夹角是