题目内容
已知A（1，2，-1），B（2，0，2），在xOy平面内的点M到A点与到B点等距离，求M点的轨迹方程 ．
考点：空间两点间的距离公式,轨迹方程
专题：计算题,空间位置关系与距离
分析：设空间任一点（x，y，z），则有：（x+1）2+（y-1）2+（z-0）2=（x-2）2+（y+1）2+（z+1）2整理即得．
解答：
解：设xOy平面内的点M（x，y，0），（z=0），
由题意点M到A点与到B点等距离得：（x+1）2+（y-2）2+（0+1）2=（x-2）2+（y-0）2+（0-2）2
整理后轨迹方程是：6x-4y-3=0，（z=0）．
故答案是：6x-4y-3=0，（z=0）．
由题意点M到A点与到B点等距离得：（x+1）2+（y-2）2+（0+1）2=（x-2）2+（y-0）2+（0-2）2
整理后轨迹方程是：6x-4y-3=0，（z=0）．
故答案是：6x-4y-3=0，（z=0）．
点评：本题主要考查空间轨迹问题，关键是利用空间任意两点间的距离公式，注意z=0不可以遗漏．属于中档题．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
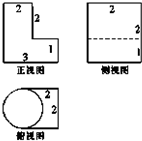
已知一个几何体的三视图如图所示，则这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
直线在平面外是指（ ）
| A、直线与平面没有公共点 |
| B、直线与平面相交 |
| C、直线与平面平行 |
| D、直线与平面最多只有一个公共点 |
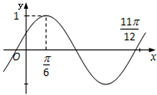函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、y=sin(2x+
| ||
B、y=sin(2x-
| ||
C、y=cos(2x+
| ||
D、y=cos(2x-
|
为了了解某班在全市“一检”中数学成绩的情况，按照分层抽样分别抽取了10名男生和5名女生的试卷成绩作为样本，他们数学成绩的茎叶图如图所示，其中茎为百位数和十位数，叶为个位数．