题目内容

函数f（x）=sin2（x+
π
4
）-sin2（x-
π
4
），x∈（
π
6
，
π
3
）的值域是
 
．
考点：三角函数中的恒等变换应用
专题：计算题,三角函数的图像与性质
分析：利用三角函数中的恒等变换可求得f（x）=sin2x，x∈（
π
6
，
π
3
）⇒2x∈（
π
3
，
2π
3
），利用正弦函数的单调性与最值即可求得其值域．
解答： 解：∵f（x）=sin2（x+
π
4
）-sin2（x-
π
4
）
=
1-cos2(x+
π
4
)
2
-
1-cos2(x-
π
4
)
2

=
1
2
（sin2x+sin2x）
=sin2x，
∵x∈（
π
6
，
π
3
），
∴2x∈（
π
3
，
2π
3
），
∴
3
2
＜sin2x≤1，
即当x∈（
π
6
，
π
3
）时，函数f（x）=sin2（x+
π
4
）-sin2（x-
π
4
）的值域是（
3
2
，1]．
故答案为：（
3
2
，1]．
点评：本题考查二倍角的余弦与诱导公式，着重考查正弦函数的单调性与最值，属于中档题．
练习册系列答案
相关题目
已知 f（x）=sinx（
3
cosx-sinx）．
（Ⅰ）求f（x）的单调增区间；
（Ⅱ）当x∈（0，
2π
3
）时，求f（x）的取值范围．
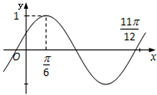函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则函数y=f（x）对应的解析式为（　　）
A、y=sin(2x+
π
6
)
B、y=sin(2x-
π
6
)
C、y=cos(2x+
π
6
)
D、y=cos(2x-
π
6
)
为了了解某班在全市“一检”中数学成绩的情况，按照分层抽样分别抽取了10名男生和5名女生的试卷成绩作为样本，他们数学成绩的茎叶图如图所示，其中茎为百位数和十位数，叶为个位数．
（Ⅰ）若该样本男女生平均分数相等，求x的值；
（Ⅱ）若规定120分以上为优秀，在该5名女生试卷中每次都抽取1份，且不重复抽取，直到确定出所有非优秀的女生为止，记所要抽取的次数为ξ，求ξ的分布列和数学期望Eξ．
设函数f(x)=
2x， x＜0
g(x)，  x＞0
，若f（x）是奇函数，则g（2）的值是
 
．
已知sinα=
5
5
，则cos2α=
 
．
已知函数f(x)=cos2
π
2
x+
3
sin
π
2
xcos
π
2
x-2，则函数f（x）在[-1，1]上的单调增区间为（　　）
A、[-
2
3
，
1
3
]
B、[-1，
1
2
]
C、[
1
3
，1]
D、[-
3
4
，
2
3
]
已知数列{an}中，a1=t（t为非零常数），{an}的前n项和Sn满足Sn+1=3Sn．
（Ⅰ）当t=1时，求数列{an}的通项公式；
（Ⅱ）若对任意n∈N*，都有λ＞
n(n+1)
an
，求实数λ的取值范围．
已知M（3，-2），点N（x，y）为直线3x+4y-25=0上任意一点，
（1）求|MN|的最小值；
（2）求
x2+y2
的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网