题目内容

在同一直角坐标系中，经过伸缩变换
x′=5x
y′=3y
后，曲线C变为曲线x′2+y′2=1，则曲线C的方程为（　　）
A、25x2+9y2=1
B、9x2+25y2=1
C、25x+9y=1
D、
x2
25
+
y2
9
=1
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：伸缩变换
x′=5x
y′=3y
，代入曲线x′2+y′2=1，化简可求曲线C的方程．
解答： 解：∵经过伸缩变换
x′=5x
y′=3y
后，曲线C变为曲线x′2+y′2=1，
∴（5x）2+（3y）2=1，
∴25x2+9y2=1．
故选A．
点评：本题考查了伸缩变换，弄清变化公式的意义和求解的方程即可，较简单．
练习册系列答案
相关题目
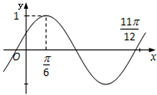函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示，则函数y=f（x）对应的解析式为（　　）
A、y=sin(2x+
π
6
)
B、y=sin(2x-
π
6
)
C、y=cos(2x+
π
6
)
D、y=cos(2x-
π
6
)
已知函数f(x)=cos2
π
2
x+
3
sin
π
2
xcos
π
2
x-2，则函数f（x）在[-1，1]上的单调增区间为（　　）
A、[-
2
3
，
1
3
]
B、[-1，
1
2
]
C、[
1
3
，1]
D、[-
3
4
，
2
3
]
已知数列{an}中，a1=t（t为非零常数），{an}的前n项和Sn满足Sn+1=3Sn．
（Ⅰ）当t=1时，求数列{an}的通项公式；
（Ⅱ）若对任意n∈N*，都有λ＞
n(n+1)
an
，求实数λ的取值范围．
在平面内，若三角形的面积为S，周长为C，则此三角形的内切圆的半径r=
2S
C
；在空间中，三棱锥P-ABC的三条侧棱PA，PB，PC两两垂直，且PA=PB=PC=1，利用类比推理的方法，求得此三棱锥P-ABC的内切球（球面与三棱锥的各个面均相切）的半径R=
 
．
已知△ABC三个顶点在同一个球面上，∠BAC=90°，AB=AC=2，若球心到平面ABC距离为1，则该球体积为（　　）
A、2
3
π
B、4
3
π
C、6
3
π
D、8
3
π
在10个同样型号的产品中，有8个是正品，2个是次品，从中任取3个，求：
（1）其中所含次品数ξ的期望、方差；
（2）事件“含有次品”的概率．
已知M（3，-2），点N（x，y）为直线3x+4y-25=0上任意一点，
（1）求|MN|的最小值；
（2）求
x2+y2
的最小值．
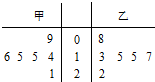甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，x1，x2分别表示甲乙两名运动员这项测试成绩的众数，s1，s2分别表示甲乙两名运动员这项测试成绩的标准差，则有（　　）
A、x1＞x2，s1＜s2
B、x1=x2，s1＜s2
C、x1=x2，s1=s2
D、x1=x2，s1＞s2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网