题目内容
19．
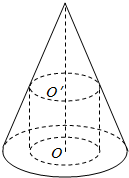如图，圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′，下底面在圆锥SO的底面上，设圆柱OO′的体积为V1，圆锥SO的体积为V2，则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$．
分析 设出圆锥的底面半径和高，分别求出圆柱和圆锥的体积，计算出比值．
解答 解：设圆锥SO的底面半径为r，高为h，则圆柱O′O的底面半径是$\frac{r}{2}$，高为$\frac{h}{2}$，
∴V2=$\frac{1}{3}$πr2h，V1=π（$\frac{r}{2}$）2•$\frac{h}{2}$=$\frac{π{r}^{2}h}{8}$，∴$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$．
故答案为$\frac{3}{8}$．
点评 本题考查了柱体和椎体的体积计算，属于基础题．
练习册系列答案
相关题目