题目内容
4．设z=$\sqrt{2}$i（1+i）3（a-i）2且z在复平面内对应的点与原点的距离为12，则实数a=$±\sqrt{3\sqrt{2}-1}$．分析 利用复数代数形式的乘法运算展开并化简，再由复数的模等于12列式求得a值．
解答 解：z=$\sqrt{2}$i（1+i）3（a-i）2=$\sqrt{2}i（-2+2i）（{a}^{2}-1-2ai）$=$-2\sqrt{2}[（{a}^{2}-1+2a）+（{a}^{2}-1-2a）i]$，
由题意可知，|z|=$2\sqrt{2}\sqrt{（{a}^{2}-1+2a）^{2}+（{a}^{2}-1-2a）^{2}}=12$，
整理得：${a}^{2}=3\sqrt{2}-1$，
∴$a=±\sqrt{3\sqrt{2}-1}$．
故答案为：$±\sqrt{3\sqrt{2}-1}$．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
相关题目
14．哈尔滨市投资修建冰雪大世界，为了调查此次修建冰雪大世界能否收回成本，组委会成立了一个调查小组对国内参观冰雪大世界的游客的消费指数（单位：百元）进行调查，在调查的1000位游客中有100位哈尔滨本地游客，把哈尔滨本地游客记为A组，内外地游客记为B组，按分层抽样从这1000人中抽取A，B组人数如下表：
A组：
B组：
（1）确定a的值，再分别在答题纸上完成A组与B组的频率分布直方图；
（2）分别估计A，B两组游客消费指数的平均数，并估计被调查的1000名游客消费指数的平均数．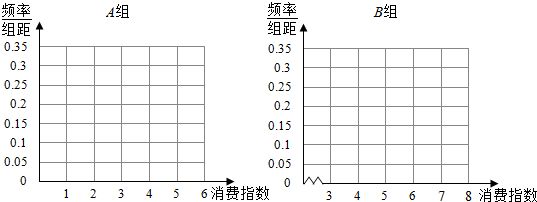
A组：
| 消费指数（百元） | [1，2） | [2，3） | [3，4） | [4，5） | [5，6） |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数（百元） | [3，4） | [4，5） | [5，6） | [6，7） | [7，8] |
| 人数 | 9 | 36 | a | 54 | 9 |
（2）分别估计A，B两组游客消费指数的平均数，并估计被调查的1000名游客消费指数的平均数．
15．已知实数a，b满足2a2-5lna-b=0，c∈R，则$\sqrt{（a-c）^{2}+（b+c）^{2}}$的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{3\sqrt{2}}{2}$ | D． | $\frac{9}{2}$ |
12．设F1、F2是双曲线x2-$\frac{{y}^{2}}{4}$=1的左、右两个焦点，在双曲线右支上取一点P，使|OP|=|PF2|（O为坐标原点）且|PF1|=λ|PF2|，则实数λ的值为（ ）
| A． | $\frac{7}{3}$ | B． | 2或$\frac{1}{2}$ | C． | 3 | D． | 2 |
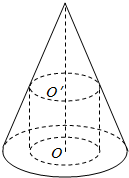如图，圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′，下底面在圆锥SO的底面上，设圆柱OO′的体积为V1，圆锥SO的体积为V2，则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$．
14．若角960°的终边上有一点（-4，a），则a的值是（ ）
| A． | 4$\sqrt{3}$ | B． | -4$\sqrt{3}$ | C． | ±4$\sqrt{3}$ | D． | $\sqrt{3}$ |