题目内容
11．已知数列{an}的通项公式是an=1-$\frac{1}{n}$，求证该数列是递增数列．分析 ?n∈N*，作差只要证明an+1-an＞0即可．
解答 证明：?n∈N*，an+1-an=$1-\frac{1}{n+1}$-$（1-\frac{1}{n}）$=$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n（n+1）}$＞0，
∴an+1＞an，
∴该数列是递增数列．
点评 本题考查了数列的单调性、“作差法”，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
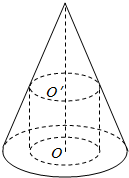如图，圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′，下底面在圆锥SO的底面上，设圆柱OO′的体积为V1，圆锥SO的体积为V2，则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$．
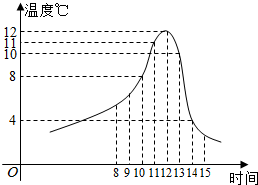某食品的保鲜时间t（单位：小时）与储藏温度x（单位：℃）满足函数关系t=$\left\{\begin{array}{l}{64，x≤0}\\{{2}^{kx+6}，x＞0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时．已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时间变化如图所示，给出以下四个结论：