题目内容
9.已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,$SA=4\sqrt{3}$,AB=2,AC=4,∠BAC=60°,则球O的表面积为( )| A. | 4π | B. | 12π | C. | 16π | D. | 64π |
分析 由三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,$SA=4\sqrt{3}$,AB=2,AC=4,∠BAC=60°,知BC=2$\sqrt{3}$,∠ABC=90°.故△ABC截球O所得的圆O′的半径r=2,由此能求出球O的半径,从而能求出球O的表面积.
解答 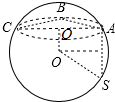 解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,
解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,
∵SA⊥平面ABC,$SA=4\sqrt{3}$,AB=2,AC=4,∠BAC=60°,
∴BC=$\sqrt{4+16-2×2×4×cos60°}$=2$\sqrt{3}$,
∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=2,
∴球O的半径R=4,
∴球O的表面积S=4πR2=64π.
故选:D.
点评 本题考查球的表面积的求法,合理地作出图形,数形结合求出球半径,是解题时要关键.

练习册系列答案
相关题目
20.判断下列各对直线的位置关系,如果相交,求出交点坐标:
(1)l1:2x-y+7=0,l2:x+y=1;
(2)${l_1}:x-3y-10=0,\;\;{l_2}:y=\frac{x+5}{3}$.
(1)l1:2x-y+7=0,l2:x+y=1;
(2)${l_1}:x-3y-10=0,\;\;{l_2}:y=\frac{x+5}{3}$.
17.下列函数中,既是奇函数又存在零点的函数是( )
| A. | y=sinx | B. | y=cosx | C. | y=lnx | D. | y=x3+1 |
14.哈尔滨市投资修建冰雪大世界,为了调查此次修建冰雪大世界能否收回成本,组委会成立了一个调查小组对国内参观冰雪大世界的游客的消费指数(单位:百元)进行调查,在调查的1000位游客中有100位哈尔滨本地游客,把哈尔滨本地游客记为A组,内外地游客记为B组,按分层抽样从这1000人中抽取A,B组人数如下表:
A组:
B组:
(1)确定a的值,再分别在答题纸上完成A组与B组的频率分布直方图;
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.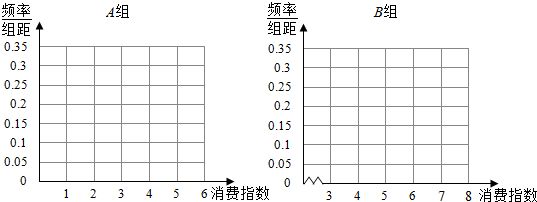
A组:
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
(2)分别估计A,B两组游客消费指数的平均数,并估计被调查的1000名游客消费指数的平均数.

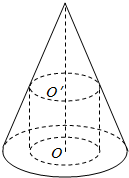 如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.
如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.