题目内容
已知函数f(x)=
,若命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,求实数k的取值范围.
|
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用,简易逻辑
分析:分析x<1的函数的单调区间,画出函数f(x)的图象,命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,即为任意t∈R,且t≠0,使得f(t)<kt恒成立,作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),求出切点和斜率,设直线与y=x(x-1)2(x≤0)图象相切于点(0,0),则有切线斜率k=1,再由图象观察即可得到范围.
解答:
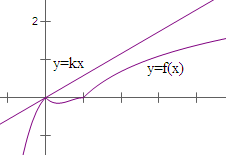 解:当x<1时,f(x)=-|x(x-1)2|=
解:当x<1时,f(x)=-|x(x-1)2|=
,
当x<0,f′(x)=(x-1)(3x-1)>0,则有f(x)得递增,
当0≤x<1,f′(x)=-(x-1)(3x-1),则区间(0,
)递减,
(
,1)递增,
画出函数y=f(x)在R上的图象,如右:
命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,
即为任意t∈R,且t≠0,使得f(t)<kt恒成立,
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),
则由(lnx)′=
,得到k=
,lnm=km,解得,m=e,k=
;
设直线与y=x(x-1)2(x≤0)图象相切于点(0,0),
则y′=[x(x-1)2]′=(x-1)(3x-1),则有k=1,
由图象可得,当直线绕着原点旋转时,转到与与y=lnx(x≥1)图象相切,
以及与y=x(x-1)2(x≤0)图象相切时,直线恒在上方,即f(t)<kt恒成立,
故实数k的取值范围是(
,1).
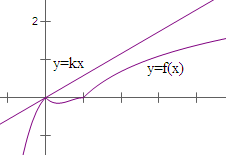 解:当x<1时,f(x)=-|x(x-1)2|=
解:当x<1时,f(x)=-|x(x-1)2|=
|
当x<0,f′(x)=(x-1)(3x-1)>0,则有f(x)得递增,
当0≤x<1,f′(x)=-(x-1)(3x-1),则区间(0,
| 1 |
| 3 |
(
| 1 |
| 3 |
画出函数y=f(x)在R上的图象,如右:
命题“存在t∈R,且t≠0,使得f(t)≥kt“是假命题,
即为任意t∈R,且t≠0,使得f(t)<kt恒成立,
作出直线y=kx,设直线与y=lnx(x≥1)图象相切于点(m,lnm),
则由(lnx)′=
| 1 |
| x |
| 1 |
| m |
| 1 |
| e |
设直线与y=x(x-1)2(x≤0)图象相切于点(0,0),
则y′=[x(x-1)2]′=(x-1)(3x-1),则有k=1,
由图象可得,当直线绕着原点旋转时,转到与与y=lnx(x≥1)图象相切,
以及与y=x(x-1)2(x≤0)图象相切时,直线恒在上方,即f(t)<kt恒成立,
故实数k的取值范围是(
| 1 |
| e |
点评:本题考查分段函数及运用,考查分段函数的图象及直线与图象之间的关系,考查存在性命题与全称性命题的转化,考查不等式的恒成立问题转化为函数图象之间的关系,是一道综合题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知在△ABC中,cos 2
=
,则△ABC的形状是( )
| A |
| 2 |
| b+c |
| 2c |
| A、直角三角形 |
| B、等腰直角三角形或直角三角形 |
| C、正三角形 |
| D、等腰直角三角形 |
空间直线a、b、c,则下列命题中真命题的是( )
| A、若a⊥b,c⊥b,则a∥c |
| B、若a与b是异面直线,b与c是异面直线,则a与c也是异面直线 |
| C、若a∥c,c⊥b,则a⊥b |
| D、若a∥b,b与c是异面直线,则a与c也是异面直线 |